Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi ![]() là không gian mẫu.
là không gian mẫu.
Ta có ![]()
Gọi D là biến cố: lấy được 2 quả cầu không trắng.
Ta có
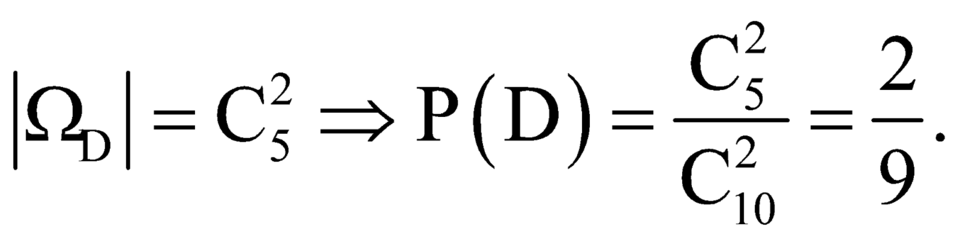

Chọn A
Số cách lấy ra 6 quả cầu từ 10 quả cầu là ![]()
![]()
Gọi A là biến cố ‘‘Trong 6 quả cầu lấy ra có không quá 1 quả cầu trắng”.
![]() là biến cố‘‘Trong 6 chi tiết lấy ra có 2 quả cầu trắng”.
là biến cố‘‘Trong 6 chi tiết lấy ra có 2 quả cầu trắng”.
Số cách lấy 4 quả cầu từ 6quả cầu đỏ và vàng là ![]() .
.
Số cách lấy 2 quả cầu trắng là ![]() .
.
Theo quy tắc nhân ta có ![]() .
.
Vậy xác suất
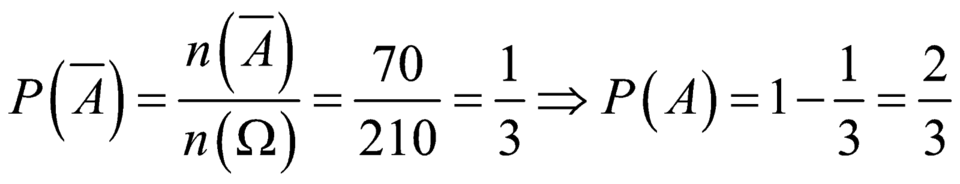 .
.

Phép thử : Chọn ngẫu nhiên bốn quả cầu
Ta có ![]()
Biến cố A: Được hai quả xanh, hai quả trắng
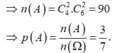
Chọn B.

a) Vì số bi trong hộp thứ nhất và hộp thứ hai là độc lập và việc lấy ra số các bi từ hai hộp là độc lập nên hai biến cố A, B là độc lập.
b)
- Trên A:
+ Hai quả lấy ra đều màu đỏ: \(P=\frac{C^2_3}{C^2_5}=\frac{3}{10}\).
+ Hai quả lấy ra cùng màu: \(P=\frac{C^2_3+C^2_2}{C^2_5}=\frac{4}{10}\)
+ Hai quả lấy ra khác màu: \(P=1-\frac{4}{10}=\frac{6}{10}\).
- Trên B:
+ Hai quả lấy ra đều màu đỏ: \(P=\frac{C^2_4}{C^2_{10}}=\frac{2}{15}\).
+ Hai quả lấy ra cùng màu: \(P=\frac{C^2_4+C^2_6}{C^2_{10}}=\frac{7}{15}\)
+ Hai quả lấy ra khác màu: \(P=1-\frac{7}{15}=\frac{8}{15}\).

Chọn A
Xếp ngẫu nhiên 6 quả cầu đôi một khác nhau thành một hàng ngang có 6! cách xếp.
Gọi A là biến cố “2 quả cầu màu trắng không xếp cạnh nhau”.
Suy ra A ¯ là biến cố “2 quả cầu màu trắng xếp cạnh nhau”.
Ta có n( A ¯ ) = 2.5!. Vậy xác suất cần tìm là