Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ˆB3B3^
b) ˆB2B2^
c) 1800 ; là cặp góc trong cùng phía
d) Bằng cặp góc so le trong ˆB2B2^=ˆA4A4^.
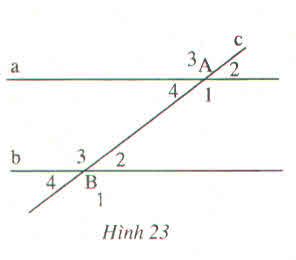
a) \(\widehat{A_1}\)\(=\widehat{B_3}\)(vì là cặp góc so le trong)
b)\(\widehat{A_2}\)\(=\widehat{B_2}\)(vì là cặp góc đồng vị)
c)\(\widehat{B_3}\)\(+\widehat{A_4}\)\(=180^0\)(vì là cặp góc trong cùng phía)
d)\(\widehat{A_2}\)\(=\widehat{B_4}\)(vì là cặp góc cùng bằng \(\widehat{A_4}\) )
Ủng hộ mk nhé!!! ^.^

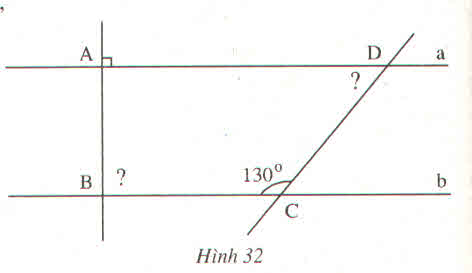
Ta có a // b, nên
góc B = góc A = 90 độ (đồng vị)
Ta lại có \(\widehat{C}+\widehat{D}=180^o\)
hay \(130^o+\widehat{D}=180^o\Rightarrow\widehat{D}=180^o-130^o=50^o\)
vậy góc B = 90 độ
góc C = 50 độ

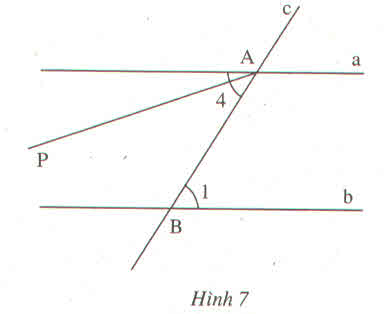
a) ˆIPOIPO^ và ˆPORPOR^ là một cặp góc so le trong..........
b) ˆOPIOPI^ và ˆTNOTNO^ là một cặp góc .....đồng vị.....
c) ˆPIOPIO^ và ˆNTONTO^ là một cặp góc ....đồng vị.....
d) ˆOPROPR^ và ˆPOIPOI^ là một .cặp góc so le trong
.........

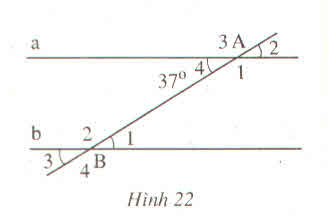
Vì a // b nên ta có:
a) ^B1 = ^A4 = 37° (2 góc so le trong)
Vậy ^B1 = 37°.
b) ^A1 = ^B4 (2 góc đồng vị).
c) ^B2 + ^A4 = 180° (2 góc trong cùng phía)
hay ^B2 + 37° =180°.
=> ^B2 = 180° - 37° = 143°.
Vậy ^B2 = 143°.

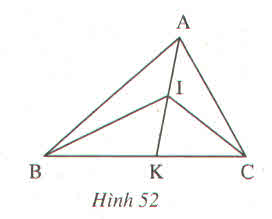
a)Ta có \(\widehat{BIK}\) là góc ngoài của BAI.
Nên \(\widehat{BIK}>\widehat{BAI}\) (1)
b) \(\widehat{CIK}>\widehat{CAI}\)( Góc ngoài của \(\Delta\) CAI)
Từ (1) và (2) ta có:
\(\widehat{BIK}+\widehat{CIK}>\widehat{BAI}+\widehat{CAI}\)
\(\Rightarrow\widehat{BIC}>\widehat{BAC}\)
) Ta có ∠BIK là góc ngoài của ∠BAI( hay là góc ngoài ∠BAK)
Các em lưu ý nếu không hiểu: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó (ở đây là tam giác ∆ BIA)
Nên ∠BIK > ∠BAK (1)
b) Góc ∠CIK > ∠CAI (2) (Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có: ∠BIK + ∠CIK > ∠BAK + ∠CAI
Mà ∠BIC = ∠BIK + ∠CIK; ∠BAC = ∠BAK + ∠CAI
⇒ ∠BIC > ∠BAC.

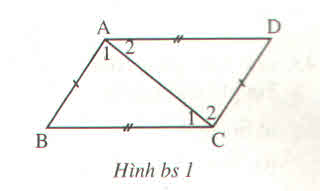
\(\widehat{A}_1=\widehat{C}_2;\widehat{A}_2=\widehat{C}_1;\widehat{B}=\widehat{D}\)

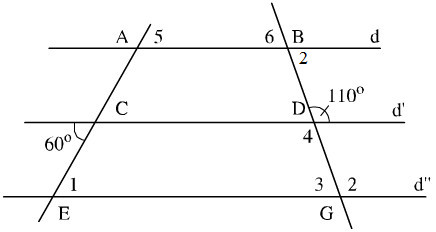
Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì d’ //d’’ có: \(\widehat{E}_1\) và góc 600 là hai góc so le trong nên \(\widehat{E}_1\)= 600
+Vì d’ // d’’ có: \(\widehat{G}_2\)và góc 1100 là hai góc đồng vị nên \(\widehat{G_2}\) = 1100
+ \(\widehat{G}_2\)+\(\widehat{G}_3\)=\(180^0\) (hai góc kề bù)
Nên \(\widehat{G_3}=180^0-\widehat{G}_2=180^0-110^0=70^0\)
+) \(\widehat{D}_4\)1100 (vì là hai góc đối đỉnh)
+) \(\widehat{A}_5\) = \(\widehat{A}_1\) (Hai góc đối đỉnh)
Mà \(\widehat{A}_1\)= 600 (vì là hai góc đồng vị)
Nên \(\widehat{A}_5\) = 600 .
+ \(\widehat{B}_6\) = \(\widehat{B}_2\)(vì là hai góc đối đỉnh)
Mà \(\widehat{B}_2\) + 1100 = 1800 (hai góc trong cùng phía)
Nên \(\widehat{B}_2\) = 1800 - 1100 = 700.
Do đó: \(\widehat{B}_6\) = 700
a) Năm cặp đường thẳng vuông góc là:
d3 ⊥ d4; d3 ⊥ d5; d3 ⊥ d7; d1 ⊥ d8; d1 ⊥ d2
b) Bốn cặp đường thẳng song song là: d4//d5; d5//d7; d4//d7; d8//d2
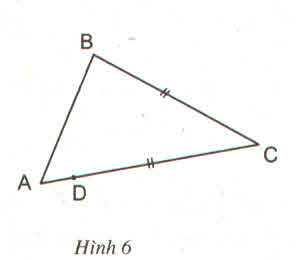







Kết luận đúng là c vì AC > BC nên ˆB>ˆAB^>A^