Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Tứ giác 1 chỉ có một cặp cạnh song song
b) Tứ giác 3 có hai cặp cạnh song song
c) Tứ giác 1 và tứ giác 3 là hình thang
a. Tứ giác 1 chỉ có một cặp cạnh song song ;
b. Tứ giác 3 có hai cặp cạnh song song ;
c. Tứ giác 1 và 3 là hình thang.
a:
Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
b:
Xét ΔABD và ΔCDB có
AB=CD
\(\hat{ABD}=\hat{CDB}\) (hai góc so le trong, AB//CD)
BD chung
Do đó: ΔABD=ΔCDB
=>\(\hat{ADB}=\hat{CBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
Định lý 2 (phát biểu)
a) Nếu tứ giác có hai cặp cạnh đối bằng nhau (theo độ dài) thì tứ giác đó là hình bình hành.
b) Nếu tứ giác có **một cặp cạnh đối vừa song song vừa bằng nhau thì tứ giác đó là hình bình hành.
Ký hiệu chung cho cả hai phần
Gọi tứ giác \(A B C D\) theo thứ tự (cạnh \(A B , B C , C D , D A\)).
Gọi \(A C\) là một đường chéo.
Cách vẽ hình minh họa (vẽ tay):
- Vẽ tứ giác bất kì \(A B C D\) (không bắt buộc là hình bình hành).
- Vẽ đường chéo \(A C\).
- Đánh dấu các cạnh bằng nhau hoặc song song theo đề bài (dấu “=” cho bằng, mũi tên song song cho song song).
- Ta sẽ dùng hai tam giác \(\triangle A B C\) và \(\triangle C D A\) để so sánh.
Phần (a) — Chứng minh:
Giả thiết: \(A B = C D\) và \(B C = A D\).
Phải chứng minh: \(A B \parallel C D\) và \(B C \parallel A D\) (tức là \(A B C D\) là hình bình hành).
Chứng minh:
- Xét hai tam giác \(\triangle A B C\) và \(\triangle C D A\).
- \(A B = C D\) (giả thiết).
- \(B C = A D\) (giả thiết).
- \(A C\) là cạnh chung.
Vậy theo tiêu chí SSS (ba cạnh bằng nhau), ta có \(\triangle A B C \cong \triangle C D A\).
- Từ đồng dư hai tam giác, các góc tương ứng bằng nhau. Cụ thể:
- \(\angle B A C = \angle D C A\).
- \(\angle B C A = \angle D A C\).
- Quan sát: \(\angle B A C\) là góc giữa đường thẳng \(B A\) và \(A C\); \(\angle D C A\) là góc giữa đường thẳng \(D C\) và \(C A\). Vì hai góc ấy bằng nhau và cùng liên quan đến đường thẳng \(A C\), suy ra đường thẳng \(B A\) song song với đường thẳng \(D C\), tức \(A B \parallel C D\).
Tương tự, từ \(\angle B C A = \angle D A C\) suy ra \(B C \parallel A D\). - Vậy hai cặp cạnh đối của \(A B C D\) song song nhau nên \(A B C D\) là hình bình hành. □
Phần (b) — Chứng minh:
Giả thiết: Một cặp cạnh đối (ví dụ \(A B\) và \(C D\)) song song và bằng nhau (tức \(A B \parallel C D\) và \(A B = C D\)).
Phải chứng minh: \(A B C D\) là hình bình hành (tức còn cặp cạnh kia cũng song song).
Chứng minh:
- Xét hai tam giác \(\triangle A B C\) và \(\triangle C D A\) như trên.
- \(A B = C D\) (giả thiết).
- \(A C\) là cạnh chung.
- Vì \(A B \parallel C D\), nên góc giữa \(B A\) và \(A C\) bằng góc giữa \(D C\) và \(C A\). Tức \(\angle B A C = \angle D C A\).
- Ta có trong hai tam giác \(\triangle A B C\) và \(\triangle C D A\):
- Một cạnh bằng (\(A B = C D\)),
- Một cạnh chung (\(A C\)),
- Góc giữa hai cạnh này bằng (\(\angle B A C = \angle D C A\)).
Do đó theo tiêu chí SAS (cạnh-góc-cạnh), \(\triangle A B C \cong \triangle C D A\).
- Từ đồng dư suy ra \(B C = A D\) (các cạnh tương ứng bằng nhau) và đồng thời các góc tương ứng bằng nhau. Do đó \(\angle B C A = \angle D A C\), suy ra \(B C \parallel A D\).
- Vì \(A B \parallel C D\) đã có và giờ \(B C \parallel A D\) vừa chứng minh, nên \(A B C D\) là hình bình hành. □
Ghi chú/trực quan hóa
- Cả hai chứng minh đều dùng đồng dư tam giác (SSS hoặc SAS) qua đường chéo \(A C\).
- Kết luận: chứng minh ra hai cạnh tương ứng song song → định nghĩa hình bình hành được thỏa mãn.
- Khi vẽ hãy:
- Vẽ \(A B C D\) và đường chéo \(A C\).
- Đánh dấu các cạnh bằng nhau (dấu “=”) hoặc mũi tên song song (nếu có song song).
- Chú thích tam giác \(\triangle A B C\) và \(\triangle C D A\) để thấy rõ các cạnh tương ứng.
Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân
Bài 2.
-Hình bn tự vẽ nhé!
Bài làm:
a, Có F là trung điểm của AC (gt)
\(\Rightarrow\)AF=\(\dfrac{1}{2}\)AC (1)
Xét tam giác ABC ta có:
E là trung điểm của AB (gt)
G là trung điểm của BC (gt)
\(\Rightarrow\)EG là đường trung bình của tam giác ABC
\(\Rightarrow\)EG=\(\dfrac{1}{2}\)AC và EG song song với AC hay EG song song với AF (2)
Từ (1) và (2)\(\Rightarrow\)AEGF là hình bình hành.
mà góc A= 90 độ (gt)\(\Rightarrow\)AEGF là hình chữ nhật.
AEGF là hcn nên có AE song song với GF ( Tính chất hcn) hay EB song song với IF (3)
mà EI song song với BF (gt) (4)
Từ (3) và (4)\(\Rightarrow\)BFIE là hình bình hành.
b, Theo a, ta có: BFIE là hình bình hành nên BE=FI (tính chất hình bình hành) và AEGF là hình chữ nhật nên AE=GF (tính chất hình chữ nhật)
mà AE=EB (E là trung điểm của AB)
\(\Rightarrow\)GF=FI.
Xét tứ giác AGCI có: FA=FC (F là trung điểm của AC), GF=FI (cmt)
\(\Rightarrow\)AGCI là hình bình hành.
mà GI vuông góc với AC nên hình bình hành AGCI là hình thoi
c, Theo b, ta có: AGCI là hình thoi
Để tứ giác (hình thoi) AGCI là hình vuông thì góc AGC= 90 độ hay AG vuông góc với BC.
Khi đó AG là đường cao của tam giác ABC
Mặt khác AC là đường trung tuyến của tam giác ABC ( G lf trung điểm của BC)\(\Rightarrow\) Tam giác ABC cân tại A
mà tam giác ABC vuông tại (gt) nên tam giác ABC vuông cân tại A thì AGCI là hình vuông.
a)Ta có E là trung điểm của CM (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) EF là đường trung bình của (định nghĩa đường trung bình của tam giác)
\(\Rightarrow\) EF//MB (tính chất đường trung bình của tam giác)
hay EF//AB
lại có K là trung điểm của AD (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) KF là đường trung bình của (...)
\(\Rightarrow\) KF//AM (t/c ...)
hay KF//AB
nên EF//KF (vì cùng // với AB)
\(\Rightarrow\) tứ giác EFFIK là hình thang (Định nghĩa hình thang)
Gọi N là trung điểm của AM, nối KM
Ta có N là trung điểm của AM (cách dựng)
K là trung điểm của AD (gt)
\(\Rightarrow\) NK là đường trung bình của
nên NK//DM (t/c....)
mà EN là đường trung bình của (E,I là trung điểm của MC,AM)
\(\Rightarrow\) EI//AC (t/c...)
lại có và
là những tam giác đều (gt)
\(\Rightarrow\)
\(\Rightarrow\) AC//DM
tức là NK//EN (cùng //AC//DM)
do đó 3 điểm E,K,N thẳng hàng (theo tiên đề Ơ-clit)
(2góc đồng vị của AC//EN)
(2 góc đồng vị của KF//AM)
nên
C/m tương tự, lấy P là trung điểm của BM ta cũng được
Hình thang EFIK có
Vậy EFIK là hình thang cân (dấu hiệu nhận biết)
b) Ta có EFIK là hình thang cân (kq câu a)
\Rightarrow EI=KF (tính chất 2 đường chéo trong hình thang cân)
E là trung điểm của CM, I là trung điểm của DM (gt)
\(\Rightarrow\) EI là đường trung bình của tam giác CMD
\(\Rightarrow\) EI=
Vậy KF=
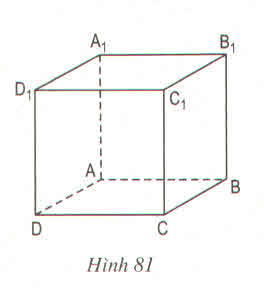
) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1
b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD
Bài 1: Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
\(\Rightarrow\)\(FG//AD\)
C/m tương tự đc \(EH//AD; GH//EF//BC\)
\(\Rightarrow EFGH\) là hình bình hành
a/Để EFGH là hình chữ nhật thì góc \(FGH=90^o\)
\(\Rightarrow góc HGD+góc FGC=90^o\)
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
\(\Rightarrow\) góc BCD+góc ADC=\(90^o\)
\(\Rightarrow\)Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=\(90^o\)
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
\(\Rightarrow\)AD=BC
\(\Rightarrow\)Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi\(\Rightarrow \)ABCD phải có đủ cả 2 điều kiện trên
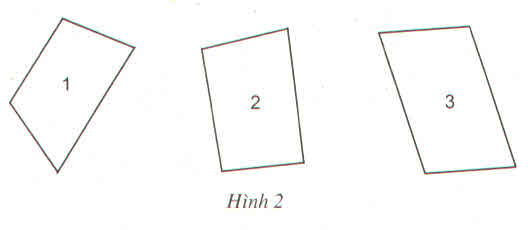
a. Tứ giác 1 có một cặp cạnh song song.
b. Tứ giác 3 có hai cặp cạnh song song.
c. Tứ giác 1 và 3 là hình thang.