Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
\(sinx+cosx+\left(sinx+cosx\right)^2+cos^2x-sin^2x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)^2+\left(cosx-sinx\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1+2cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\\1+2cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)

a/ \(y'=4\left(2x-3\right)^3.\left(2x-3\right)'=8\left(2x-3\right)^3\)
b/ \(y'=5cos^43x.\left(cos3x\right)'=-15cos^43x.sin3x\)
c/ \(y'=\frac{\left[cos\left(1-2x^2\right)\right]'}{2\sqrt{cos\left(1-2x^2\right)}}=\frac{-sin\left(1-2x^2\right).\left(1-2x^2\right)'}{2\sqrt{cos\left(1-2x^2\right)}}=\frac{2x.sin\left(1-2x^2\right)}{\sqrt{cos\left(1-2x^2\right)}}\)
d/ \(y'=\frac{\left(\frac{x+1}{x-1}\right)'}{2\sqrt{\frac{x+1}{x-1}}}=\frac{\frac{-2}{\left(x-1\right)^2}}{2\sqrt{\frac{x+1}{x-1}}}=-\frac{1}{\left(x-1\right)^2\sqrt{\frac{x+1}{x-1}}}\)
e/ \(y'=4\left(1+sin^2x\right)^3\left(1+sin^2x\right)'=8.sinx.cosx\left(1+sin^2x\right)^3=4sin2x.\left(1+sin^2x\right)^3\)

1.
\(\Leftrightarrow3x=k\pi\Leftrightarrow x=\frac{k\pi}{3}\)
2.
\(\Leftrightarrow cos5x=0\Leftrightarrow5x=\frac{\pi}{2}+k\pi\Leftrightarrow x=\frac{\pi}{10}+\frac{k\pi}{5}\)
4.
\(cos3x+cosx+cos2x=0\)
\(\Leftrightarrow2cos2x.cosx+cos2x=0\)
\(\Leftrightarrow cos2x\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cosx=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
5.
\(sin6x+sin2x+sin4x=0\)
\(\Leftrightarrow2sin4x.cos2x+sin4x=0\)
\(\Leftrightarrow sin4x\left(2cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin4x=0\\cos2x=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{4}\\x=\pm\frac{\pi}{3}+k\pi\end{matrix}\right.\)
6. ĐKXĐ; ...
\(\Leftrightarrow tanx+tan2x=1-tanx.tan2x\)
\(\Leftrightarrow\frac{tanx+tan2x}{1-tanx.tan2x}=1\)
\(\Leftrightarrow tan3x=1\)
\(\Leftrightarrow x=\frac{\pi}{12}+\frac{k\pi}{3}\)

\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\cdot\left(sin^2x+cos^2x\right)=1-\dfrac{3}{4}sin^22x\)
=>\(1-\dfrac{3}{2}\cdot sin^22x=1-\dfrac{3}{4}sin^22x\)
=>\(sin^22x=0\)
=>2x=kpi
=>x=kpi/2
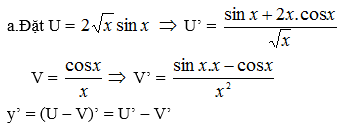
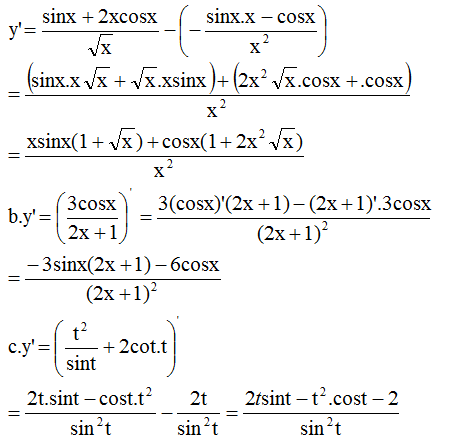
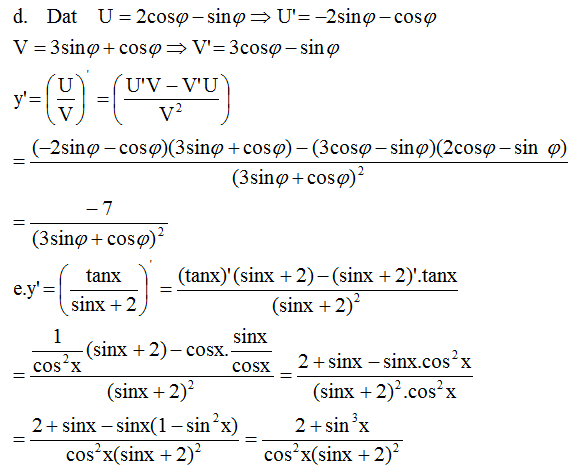
1) đặc : \(f\left(x\right)=y=cot4x\)
điều kiện xác định : \(sin4x\ne0\Leftrightarrow4x\ne k\pi\Leftrightarrow x\ne\dfrac{k\pi}{4}\)
\(\Rightarrow x\in D\) thì \(-x\in D\)
ta có : \(f\left(-x\right)=cot\left(-4x\right)=-cot4x=-f\left(x\right)\)
\(\Rightarrow\) hàm này là hàm lẽ
2) đặc : \(f\left(x\right)=y=\left|cotx\right|\)
điều kiện xác định : \(sinx\ne0\Leftrightarrow x\ne k\pi\)
\(\Rightarrow x\in D\) thì \(-x\in D\)
ta có : \(f\left(-x\right)=\left|cot\left(-x\right)\right|=\left|-cotx\right|=\left|cotx\right|=f\left(x\right)\)
\(\Rightarrow\) hàm này là hàm chẳn
3) đặc : \(f\left(x\right)=y=1-sin^2x=cos^2x\)
điều kiện xác định : \(D=R\)
\(\Rightarrow x\in D\) thì \(-x\in D\)
ta có : \(f\left(-x\right)=cos^2\left(-x\right)=cos^2x=f\left(x\right)\)
\(\Rightarrow\) hàm này là hàm chẳn
4) đặc : \(f\left(x\right)=y=sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{sinx+cosx}{\sqrt{2}}\)
điều kiện xác định : \(D=R\)
\(\Rightarrow x\in D\) thì \(-x\in D\)
ta có : \(f\left(-x\right)=\dfrac{sin\left(-x\right)+cos\left(-x\right)}{\sqrt{2}}=\dfrac{-sinx+cosx}{\sqrt{2}}\ne f\left(x\right);-f\left(x\right)\)
\(\Rightarrow\) hàm này là hàm không chẳn không lẽ
mấy bài còn lại bn làm tương tự cho quen nha