Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Parabol y = ax2 + bx + c có:
+ Tọa độ đỉnh D là:
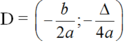
+ Phương trình trục đối xứng là:
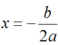

Điều kiện để (P): \(y=ax^2+bx+c\) cắt trục hoành tại hai điểm phân biệt là \(\Delta>0\).
Gọi \(x_1;x_2\) là hoành độ của hai giao điểm. Ta có:
\(x_{1,2}=\dfrac{-b\pm\sqrt{\Delta}}{2a}\);
Tọa độ giao điểm là:
\(A\left(\dfrac{-b+\sqrt{\Delta}}{2a};0\right)\); \(A\left(\dfrac{-b-\sqrt{\Delta}}{2a};0\right)\).

Lời giải
a)
a.1) Trục đối xứng y =1/4
a.2) giao trục tung A(0,-2)
a.3) giao trục hoành (\(\left(\Delta=17\right)\) \(B\left(\dfrac{1-\sqrt{17}}{4};0\right)\);\(C\left(\dfrac{1+\sqrt{17}}{4}\right)\)
b)
b.1) Trục đối xứng y =-1/4
b.2) giao trục tung A(0,2)
a.3) giao trục hoành \(\left(\Delta=17\right)\) \(B\left(\dfrac{-1-\sqrt{17}}{4};0\right)\);\(C\left(\dfrac{-1+\sqrt{17}}{4}\right)\)

a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
b) Giải hệ phương trình:
Parabol: y = x2 - x + 2.
c) Giải hệ phương trình:
Parabol: y = x2 - 4x + 2.
d) Ta có:
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 - 3x + 2.

Câu 1: (P) : \(y=ax^2+bx+c\)
Vì (P) cắt trục Ox tại hai điểm có hoành độ lần lượt là -1 và 2
nên (P) cắt hai điểm A(-1;0) và B (2;0)
A (-1;0) ∈ (P) ⇔ 0 = a - b+c (1)
B (2;0) ∈ (P) ⇔ 0 = 4a+2b+c (2)
Mà (P) cắt trục Oy tại điểm có tung độ bằng -2
nên (P) cắt C ( 0;-2)
C (0;-2) ∈ (P) ⇔ -2 = c (3)
Từ (1) ,(2) và (3) ⇔ \(\left\{{}\begin{matrix}a-b+c=0\\4a+2b+c=0\\c=-2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}a-b=2\\4a+2b=2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}a=1\\b=-1\end{matrix}\right.\)
Vậy (P) : \(y=x^2-x-2\)
Câu 2: (P) : \(y=ax^2+bx+c\)
Vì (P) có đỉnh I ( -2;-1)
⇔ \(\left\{{}\begin{matrix}\dfrac{-b}{2a}=-2\\-1=4a-2b+c\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}-4a+b=0\\4a-2b+c=-1\end{matrix}\right.\)(1)
Mà (P) cắt trục tung tại điểm có tung độ bằng -3
nên (P) cắt A( 0;-3)
A(0;-3) ∈ (P) ⇔ -3 = c (2)
Từ (1) và (2) ⇔ \(\left\{{}\begin{matrix}-4a+b=0\\4a-2b+c=-1\\c=-3\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}-4a+b=0\\4a-2b=2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}a=\dfrac{-1}{2}\\b=-2\end{matrix}\right.\)
Vậy (P) : \(y=\dfrac{-1}{2}x^2-2x-3\)

Ở đây a = 2; b = -2; c = -2. Ta có Δ = ( - 1 ) 2 - 4 . 2 . ( - 2 ) = 17
Trục đối xứng là đường thẳng x = 1/4; đỉnh I(1/4; -17/8) giao với trục tung tại điểm (0; -2).
Để tìm giao điểm với trục hoành ta giải phương trình
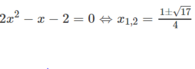
Vậy các giao điểm với trục hoành là


Trục đối xứng x = -1/4; đỉnh I(-1/4; -17/8) giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm
![]()

a) Ta có: a2 = 25 => a = 5 độ dài trục lớn 2a = 10
b2 = 9 => b = 3 độ dài trục nhỏ 2a = 6
c2 = a2 – b2 = 25 - 9 = 16 => c = 4
Vậy hai tiêu điểm là : F1(-4 ; 0) và F2(4 ; 0)
Tọa độ các đỉnh A1(-5; 0), A2(5; 0), B1(0; -3), B2(0; 3).
b)
4x2 + 9y2 = 1 <=> +
= 1
a2= => a =
=> độ dài trục lớn 2a = 1
b2 = => b =
=> độ dài trục nhỏ 2b =
c2 = a2 – b2
= -
=
=> c =
F1(- ; 0) và F2(
; 0)
A1(-; 0), A2(
; 0), B1(0; -
), B2(0;
).
c) Chia 2 vế của phương trình cho 36 ta được :
=> +
= 1
Từ đây suy ra: 2a = 6. 2b = 4, c =\(\sqrt{5}\)
=> F1(-\(\sqrt{5}\) ; 0) và F2(\(\sqrt{5}\) ; 0)
A1(-3; 0), A2(3; 0), B1(0; -2), B2(0; 2).


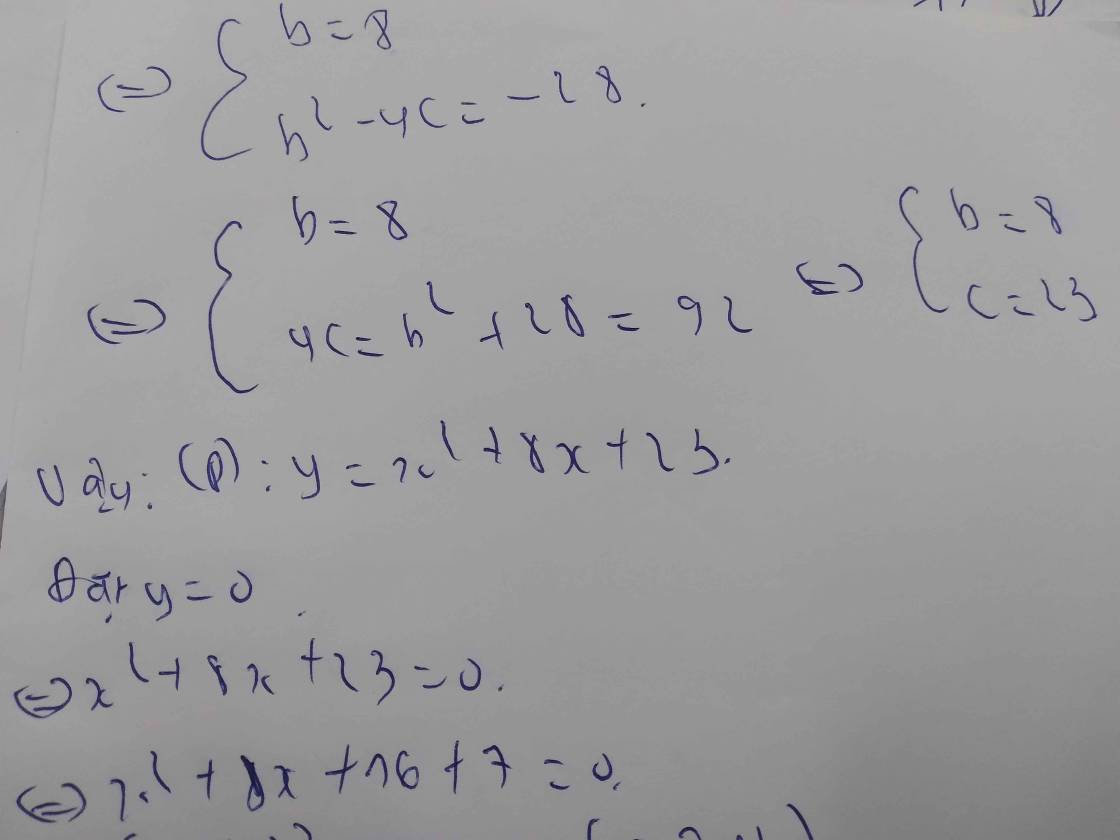
Tọa độ đỉnh \(\left(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\right)\)
Trục đối xứng \(x=\dfrac{-b}{2a}\)