HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
11 tháng 5 2018
+ Parabol y = ax2 + bx + 2 đi qua điểm B(–1 ; 6)
⇒ 6 = a.( –1)2 + b.( –1) + 2 ⇒ a = b + 4 (1)
+ Parabol y = ax2 + bx + 2 có tung độ của đỉnh là –1/4
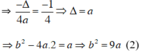
Thay (1) vào (2) ta được: b2 = 9.(b + 4) ⇔ b2 – 9b – 36 = 0.
Phương trình có hai nghiệm b = 12 hoặc b = –3.
Với b = 12 thì a = 16.
Với b = –3 thì a = 1.
Vậy có hai parabol thỏa mãn là y = 16x2 + 12b + 2 và y = x2 – 3x + 2.
VH
12 tháng 10 2020
Đỉnh của parabol là \(\frac{-\Delta}{4a}\) ta có
\(\left\{{}\begin{matrix}\frac{-\Delta}{4a}=-25\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\24a+c=0\\2a+b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a^2-4ac=100a\\24a+c=0\\b=-2a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-c=25\\24a+c=0\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=-24\end{matrix}\right.\)
\(\Rightarrow y=x^2-2x-24\)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Đồ thị hàm số \(y = a{x^2} + bx + 1\) đi qua điểm A(1; 0) nên:
\(a{.1^2} + b.1 + 1 = 0 \Leftrightarrow a + b = - 1\)
Đồ thị hàm số \(y = a{x^2} + bx + 1\) đi qua điểm B(2; 4) nên:
\(a{.2^2} + 2b + 1 = 4 \Leftrightarrow 4a + 2b = 3\)
Từ 2 phương trình trên, ta có \(a = \frac{5}{2};b = \frac{{ - 7}}{2}\)
=> Hàm số cần tìm là \(y = \frac{5}{2}{x^2} - \frac{7}{2}x + 1\)
b) Đồ thị hàm số \(y = a{x^2} + bx + 1\) đi qua điểm A(1; 0) nên:
\(a{.1^2} + b.1 + 1 = 0 \Leftrightarrow a + b = - 1\)
Đồ thị hàm số \(y = a{x^2} + bx + 1\) có trục đối xứng x=1
\(\frac{{ - b}}{{2a}} = 1 \Leftrightarrow - b = 2a \Leftrightarrow 2a + b = 0\)
Từ 2 phương trình trên, ta có \(a = 1;b = - 2\)
=> Hàm số cần tìm là \(y = {x^2} - 2x + 1\)
c) Đồ thị hàm số \(y = a{x^2} + bx + 1\) có đỉnh \(I(1;2)\) nên:
\(\frac{{ - b}}{{2a}} = 1 \Leftrightarrow - b = 2a \Leftrightarrow 2a + b = 0\)
\(a{.1^2} + b.1 + 1 = 2 \Leftrightarrow a + b = 1\)
Từ 2 phương trình trên, ta có \(a = - 1;b = 2\)
=> Hàm số cần tìm là \(y = - {x^2} + 2x + 1\)
d) Đồ thị hàm số \(y = a{x^2} + bx + 1\) đi qua điểm C(-1; 1) nên:
\(a.{( - 1)^2} + b.( - 1) + 1 = 1 \Leftrightarrow a - b = 0 \Leftrightarrow a = b\)
Đồ thị hàm số \(y = a{x^2} + bx + 1\) có tung độ đỉnh là -0,25 nên:
\(\frac{{ - \Delta }}{{4a}} = - 0,25 \Leftrightarrow - \frac{{{b^2} - 4.a.1}}{{4a}} = - 0,25 \Leftrightarrow {b^2} - 4a = a \Leftrightarrow {b^2} = 5a\)
Thay a=b ta có:
\({b^2} = 5b \Leftrightarrow b=0\) hoặc \(b=5\)
Vì \(a \ne 0\) nên \(a=b=5\)
=> Hàm số cần tìm là \(y = 5{x^2} + 5x + 1\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2023
Từ điều kiện đề bài: (hiển nhiên a khác 0):
\(\left\{{}\begin{matrix}\dfrac{4ac-b^2}{4a}=-1\\a-b+c=7\\c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a-b^2=-4a\\a-b=6\\c=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-6\right)^2-8a=0\\b=a-6\\c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\left\{2;18\right\}\\b=a-6\\c=1\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=2x^2-4x+1\\y=18x^2+12x+1\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
\(\left\{{}\begin{matrix}\dfrac{4ac-b^2}{4a}=1\\4a+2b+c=0\\4a-2b+c=-8\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4ac-b^2=4a\\4a+2b+c=0\\4b=8\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=2\\4ac-4=4a\\4a+4+c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=2\\ac-1=a\\c=-4a-4\end{matrix}\right.\)
\(\Rightarrow a\left(-4a-4\right)-1=a\)
\(\Rightarrow4a^2+5a+1=0\) \(\Rightarrow\left[{}\begin{matrix}a=-1\Rightarrow c=0\\a=-\dfrac{1}{4}\Rightarrow c=-3\end{matrix}\right.\)
Vậy có 2 pt (P): \(\left[{}\begin{matrix}y=-x^2+2x\\y=-\dfrac{1}{4}x^2+2x-3\end{matrix}\right.\)
PM
1
4 tháng 9 2021
Tìm Parabol (P): y=ax2+bx+c đi qua điểm A(1;0) và có tung độ đỉnh bằng -1
Lời giải:
ĐK: $a\neq 0$
Gọi đỉnh của parabol là $I$.
Ta có:
Hoành độ đỉnh: $x_I=\frac{-b}{2a}$
Tung độ đỉnh: $y_I=ax_I^2+bx_I+1=1-\frac{b^2}{4a}=0$
$\Rightarrow b^2=4a(*)$
Mặt khác parabol đi qua điểm $N(1,4)$ nên:
$y_N=ax_N^2+bx_N+1$
$\Leftrightarrow 4=a+b+1(**)$
Từ $(*); (**)\Rightarrow b^2=4(3-b)\Rightarrow b=2$ hoặc $b=-6$
Nếu $b=2\rightarrow a=1$. Parabol $y=x^2+2x+1$
Nếu $b=-6\rightarrow a=9$. Parabol $y=9x^2-6x+1$