Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
Nhận xét: các hàm sin, cosin là các hàm điều hòa, nên giá trị trung bình theo thời gian của các hàm này đều bằng 0.
a) 0; b) 0; c) 0;
d)
\(4sin^2100\Pi t=4\left(\dfrac{1-cos200\Pi t}{2}\right)=2-2cos200\Pi t\)
Vậy \(\overline{4sin^2100\Pi t}=\overline{2-2cos200\Pi t}=2-\overline{2cos200\Pi t}=2\);
e) 0.
Nhận xét: các hàm sin, cosin là các hàm điều hòa, nên giá trị trung bình theo thời gian của các hàm này đều bằng 0.
a) 0; b) 0; c) 0;
d) 4sin2100πt = 4(
) = 2 - 2cos200πt
Vậy = = 2 - = 2
e) 0.

Chọn đáp án D.
Vì ZC = ZL = 30Ω nên mạch cộng hưởng → i và u cùng pha.
Ta có: u = 120√2cos100πt (V) → i = I0cos100πt (A)
Với 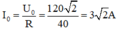
Vậy i = 3√2cos100πt (A)

Đáp án: D
Ta có: ZL = 60Ω; ZC = 20Ω
Tổng trở của mạch:
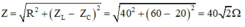
Biểu thức của i:
Ta có: u = 240√2cos100πt (V) → i = I0cos(100πt + φi)
Với 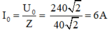
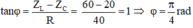
→ φ = φu – φi → φi = φu – φ = 0 – π/4 = – π/4 rad
Vậy i = 6cos(100πt – π/4) (A)

Đáp án C
+ Với đoạn mạch chỉ chứa tụ, dòng trong mạch sớm pha hơn điện áp một góc 0,5π → φ = 5π/6

Ta có: \(Z_L=L\omega=100\left(\Omega\right)\)
\(Z_C=\dfrac{1}{C\omega}=200\left(\Omega\right)\)
\(\Rightarrow Z=\sqrt{\left(R+r\right)^2+\left(Z_L-Z_C\right)^2}=100\sqrt{2}\left(\Omega\right)\)
Có: \(U_0=I_0.Z=200\sqrt{2}\left(V\right)\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R+r}=-1\) \(\Rightarrow\varphi=-\dfrac{\pi}{4}=\varphi_u-\varphi_i\) \(\Rightarrow\varphi_u=-\dfrac{5\pi}{12}\)
Vậy: \(u=200\sqrt{2}\cos\left(100\pi t-\dfrac{5\pi}{12}\right)\)
→ Đáp án: C
Bạn tham khảo nhé!

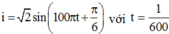
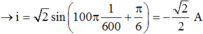
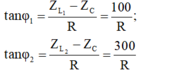
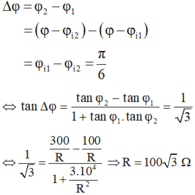
+ Ta nhận thấy các hàm:
a) 2sin100πt; b) 2cos100πt; c) 2sin(100πt + π/6 ); e) 3cos(100πt - π/3 ) đều là những hàm điều hòa dạng hình sin theo thời gian, nên giá trị trung bình của chúng đều bằng 0.
+ Với hàm
Số hạng thứ nhất lấy trung bình vẫn bằng 2, số hạng thứ hai là hàm điều hòa dạng sin theo thời gian nên giá trị trung bình bằng 0.
Vậy giá trị trung bình của hàm 4sin2100π t bằng 2.