Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=3\left(m-1\right)x^2+6mx+4m+4\)
Để hàm số đã cho đồng biến trên R \(\Leftrightarrow y'\ge0\) \(\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}3\left(m-1\right)>0\\\Delta'=\left(3m\right)^2-3\left(m-1\right)\left(4m+4\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\-3m^2+12\le0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m\ge2\)
\(\Rightarrow m=\left\{2;3;4...2019\right\}\Rightarrow\) có \(2019-2+1=2018\) giá trị nguyên

Câu 2:
ĐK: $m\not\in (-1;+\infty)$
$y=\frac{mx+4}{x+m}\Rightarrow y'=\frac{m^2-4}{(x+m)^2}$
Để $y$ nghịch biến trên khoảng $(-\infty; 1)$ thì:
\(\left\{\begin{matrix} m\not\in (-1;+\infty)\\ y'=\frac{m^2-4}{(x+m)^2}\leq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\not\in (-1;+\infty)\\ -2\leq m\leq 2\end{matrix}\right.\)
Với $m$ nguyên ta suy ra $m=-1; -2$. Vậy có 2 giá trị nguyên của $m$ thỏa mãn.
Câu 1:
Để $y$ đồng biến trên $(-\infty; +\infty)$ thì:
$y'=3x^2-2(2m-1)x+(2-m)\geq 0$ với mọi $x\in\mathbb{R}$
Điều này xảy ra khi: $\Delta'=(2m-1)^2-3(2-m)\leq 0$
$\Leftrightarrow 4m^2-m-5\leq 0$
$\Leftrightarrow (4m-5)(m+1)\leq 0$
$\Leftrightarrow -1\leq m\leq \frac{5}{4}$

HẾT RỒI NHÉ ĐÁP ÁN LÀ :
+ Ta có: y '= 3x2 + 6x + m
+ Để hàm số đã cho đồng biến trên R thì y' ≥ 0,∀x ∈R
+ Yêu cầu bài toán trở thành tìm điều kiện của m để y' ≥ 0,∀x ∈R
Ta có y' = 3x2 + 6x + m, ta có: a = 3>0,Δ = 36 - 12m
Để y' ≥ 0,∀x ∈ R khi Δ ≤ 0 ⇔ 36 - 12m ≤ 0 ⇔ m ≥ 3
Vậy giá trị của tham số m cần tìm là m ≥ 3

a) Trục Ox là đường thẳng đi qua O(0, 0, 0) và nhận i→=(1,0,0) làm vectơ chỉ phương nên có phương trình tham số là:
* Tương tự, trục Oy có phương trình
Trục Oz có phương trình
b) Đường thẳng đi qua M0 (x0,y0,z0) song song với trục Ox sẽ có vectơ chỉ phương là i→(1,0,0) nên có phương trình tham số là:
tương tự ta có Phương trình của đường thẳng đi qua M0 (x0,y0,z0) và song song với Oy là:
phương trình đường thẳng đi qua M0 (x0,y0,z0) và song song với Oz là
c) Đường thẳng đi qua M(2, 0, -1) và có vectơ chỉ phương u→(-1,3,5) có phương trình tham số là
có phương trình chính tắc là
d) Đường thẳng đi qua N(-2, 1, 2) và có vectơ chỉ phương u→(0,0,-3) có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
e) Đường thẳng đi qua N(3, 2, 1) và vuông góc với mặt phẳng: 2x- 5y + 4= 0 nên nó nhận vectơ pháp tuyến của mặt phẳng này làn→(2,-5,0) là vectơ chỉ phương, nên ta có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
f) Đường thẳng đi qau P(2, 3, -1) và Q(1, 2, 4) sẽ nhận PQ→(-1,-1,5) là vectơ chỉ phương, nên có phương trình tham số là
và có phương tình chính tắc là
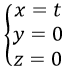
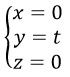
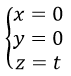
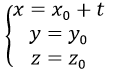
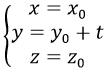
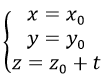
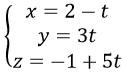
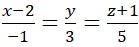
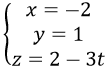
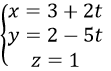
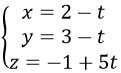
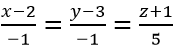
đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có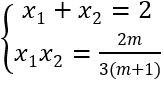
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.