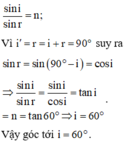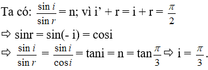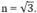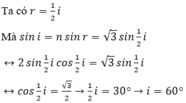Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

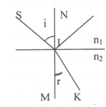
\(\sin i=n.\sin r\Rightarrow n=\dfrac{\sin i}{\sin r}\)
\(\sin i'=n.\sin r'\Rightarrow n=\dfrac{\sin i'}{\sin r'}\)
\(i+i'=90^0\Rightarrow\sin i'=\cos\left(90^0-i'\right)=\cos i\)
\(\Rightarrow\dfrac{\sin i}{\sin r}=\dfrac{\cos i}{\sin r'}\Leftrightarrow\dfrac{\sin i}{\sin30^0}=\dfrac{\cos i}{\sin45^0}\)
\(\Leftrightarrow\sin i-\dfrac{\sqrt{2}}{2}\cos i=0\)
\(\cos x=0\) ko la nghiem pt
\(\cos x\ne0\Rightarrow\tan i-\dfrac{\sqrt{2}}{2}=0\Rightarrow\tan i=\dfrac{\sqrt{2}}{2}\Rightarrow i\approx35^0\)
\(\Rightarrow n=\dfrac{\sin i}{\sin r}=\dfrac{\sin35^0}{\sin30^0}\approx1,15\)
\(\)
\(\)

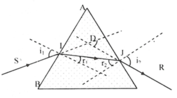
a) Áp dụng công thức lăng kính ta có:
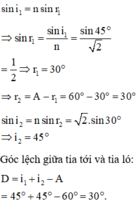
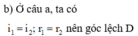
tính được ở câu a, là góc lệch cực tiểu. Do đó nếu ta tăng hoặc giảm góc tới 10 ° thì góc lệch tăng.

Ta có: sin i sin r = n ; v ì i ' + r = i + r = π 2 ⇒ sin r = sin ( - i ) = cos i
⇒ sin i sin r = sin i cos i = tan i = n = tan π 3 ⇒ i = π 3

Đáp án: A
i + r = 900 => sinr = cosi, sini = -x ∈ D, cosi => tani =![]()
=> i = 600