K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
7 tháng 4 2017

Xác định các hệ số a, b, c rồi giải phương trình : 2 x 2 - 2 2 x + 1 = 0
#Toán lớp 9
1
CM
Cao Minh Tâm
7 tháng 4 2017

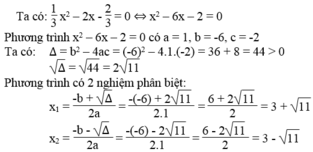
Phương trình 2 x 2  - 2 2  x + 1 = 0 có a = 2, b = -2 2 , c = 1

Ta có: ∆ = b 2  – 4ac = - 2 2 2  – 4.2.1 = 8 – 8 = 0

Phương trình có nghiệm kép :

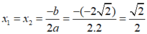
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)
PT
Pham Trong Bach
2 tháng 8 2018

Xác định các hệ số a, b, c rồi giải phương trình : 2 x 2 - (1 - 2 2 )x -  2 = 0
#Toán lớp 9
1
CM
Cao Minh Tâm
2 tháng 8 2018

Phương trình 2 x 2  – (1 - 2 2 )x -  2  = 0 có a = 2, b = -(1 - 2 2  ), c = - 2

Ta có:  ∆  =  b 2  – 4ac =  - 1 - 2 2 2  – 4.2.(- 2 )

= 1 - 4 2  + 8 + 8 2  = 1 + 4 2  + 8

= 1 + 2.2 2  +  2 2 2  =  1 + 2 2 2  > 0

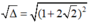Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9 = 1 + 2 2

 

Phương trình có 2 nghiệm phân biệt :

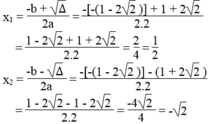
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)
SG
Sách Giáo Khoa
8 tháng 5 2017

Xác định các hệ số a, b, c rồi giải phương trình :

a) \(2x^2-2\sqrt{2}x+1=0\)

b) \(2x^2-\left(1-2\sqrt{2}\right)x-\sqrt{2}=0\)

c) \(\dfrac{1}{3}x^2-2x-\dfrac{2}{3}=0\)

d) \(3x^2+7,9x+3,36=0\)
#Toán lớp 9
1
NT
Nguyen Thuy Hoa
21 tháng 6 2017

Hàm số y = ax^2 (a khác 0). Phương trình bậc hai một ẩn

Đúng(0)
PT
Pham Trong Bach
3 tháng 1 2020

Xác định các hệ số a, b, c ; tính biệt thức  ∆  rồi tìm nghiệm của các phương trình : 5 x 2 - x + 2 = 0
#Toán lớp 9
1
CM
Cao Minh Tâm
3 tháng 1 2020

Phương trình 5 x 2  – x + 2 = 0 có a = 5, b = -1, c = 2

Ta có:  ∆ =  b 2  – 4ac =  - 1 2  – 4.5.2 = 1 – 40 = -39 < 0

Vậy phương trình vô nghiệm.

Đúng(0)
PT
Pham Trong Bach
24 tháng 9 2018

Xác định các hệ số a, b, c rồi giải phương trình : 3 x 2 + 7,9x + 3,36 = 0
#Toán lớp 9
1
CM
Cao Minh Tâm
24 tháng 9 2018

Phương trình 3 x 2  + 7,9x + 3,36 = 0 có a = 3, b = 7,9, c = 3,36

Ta có: Δ =  b 2  – 4ac =  7 , 9 2  – 4.3.3,36 = 62,41 – 40,32 = 22,09 > 0

∆ = 22 , 09 = 4,7

Phương trình có 2 nghiệm phân biệt :

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)
TN
Tâm Nguyễn
26 tháng 2 2021
Hãy viết các phương trình sau dưới dạng ax^2+bx+c=0 rồi xác định các hệ số a.b.c.của mỗi phương trình A.x^2+3-4x=m B.(2x-3/căn 2)(2x-3/căn2)=0
#Toán lớp 9
0
TN
Tâm Nguyễn
26 tháng 2 2021
Hãy viết các phương trình sau dươi dạng ax^2+bx+c=0 rồi xác định các hệ số a.b.c.của mỗi phương trình A.x^2+3-4x=m B.(2x-3/căn2)(2x-3/căn2)=0
#Toán lớp 9
0
PT
Pham Trong Bach
17 tháng 10 2017

Xác định các hệ số a, b, c ; tính biệt thức ∆  rồi tìm nghiệm của các phương trình : 2 x 2 – 5x + 1 = 0
#Toán lớp 9
1
CM
Cao Minh Tâm
17 tháng 10 2017

Phương trình 2 x 2  – 5x + 1 = 0 có a = 2, b = -5, c = 1

Ta có:  ∆  =  b 2  – 4ac =  - 5 2  – 4.2.1 = 25 – 8 = 17 > 0

∆ = 17

Phương trình có 2 nghiệm phân biệt :

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)
TN
Trúc Nguyễn
18 tháng 1 2021
bằng phương pháp thế , giải các hệ phương trình sau rồi tính nghiệm gần đúng chính xác đến hai số thập...
Đọc tiếp

bằng phương pháp thế , giải các hệ phương trình sau rồi tính nghiệm gần đúng chính xác đến hai số thập phân

a,\(\left\{{}\begin{matrix}x-\sqrt{3}y=0\\\sqrt{3}x+2y=1+\sqrt{3}\end{matrix}\right.\)

b,\(\left\{{}\begin{matrix}\sqrt{2}x-\sqrt{5}y=1\\x+\sqrt{5}y=\sqrt{2}\end{matrix}\right.\)

c,\(\left\{{}\begin{matrix}\sqrt{2}x+\sqrt{5}y=2\\x+\sqrt{5}y=2\end{matrix}\right.\)

d,\(\left\{{}\begin{matrix}x-2\sqrt{2}y=\sqrt{3}\\\sqrt{2}x+y=1-\sqrt{6}\end{matrix}\right.\)
#Toán lớp 9
1
HP
Hồng Phúc
18 tháng 1 2021

Làm mẫu hai câu a, b thôi nha.

a, \(\left\{{}\begin{matrix}x-\sqrt{3}y=0\\\sqrt{3}x+2y=1+\sqrt{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{3}y\\\sqrt{3}.\sqrt{3}y+2y=1+\sqrt{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{3}y\\5y=1+\sqrt{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\sqrt{3}+3}{5}\\y=\dfrac{1+\sqrt{3}}{5}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\approx0,95\\y\approx0,55\end{matrix}\right.\)

b, \(\left\{{}\begin{matrix}\sqrt{2}x-\sqrt{5}y=1\\x+\sqrt{5}y=\sqrt{2}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{2}\left(\sqrt{2}-\sqrt{5}y\right)-\sqrt{5}y=1\\x=\sqrt{2}-\sqrt{5}y\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2-\sqrt{5}\left(\sqrt{2}+1\right)y=1\\x=\sqrt{2}-\sqrt{5}y\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{\sqrt{2}-1}{\sqrt{5}}\\x=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y\approx0,19\\x=1\end{matrix}\right.\)

Đúng(2)
TN
Trúc Nguyễn
18 tháng 1 2021
bằng phương pháp thế , giải các hệ phương trình sau rồi tính nghiệm gần đúng chính xác đến hai số thập...
Đọc tiếp

bằng phương pháp thế , giải các hệ phương trình sau rồi tính nghiệm gần đúng chính xác đến hai số thập phân

a,\(\left\{{}\begin{matrix}x-\sqrt{3}y=0\\\sqrt{3}x+2y=1+\sqrt{3}\end{matrix}\right.\)

b,\(\left\{{}\begin{matrix}\sqrt{2}x-\sqrt{5}y=1\\x+\sqrt{5}y=\sqrt{2}\end{matrix}\right.\)

c,\(\left\{{}\begin{matrix}\sqrt{2}x+\sqrt{5}y=2\\x+\sqrt{5}y=2\end{matrix}\right.\)

d,\(\left\{{}\begin{matrix}x-2\sqrt{2}y=\sqrt{3}\\\sqrt{2}x+y=1-\sqrt{6}\end{matrix}\right.\)
#Toán lớp 9
1
T
tthnew
18 tháng 1 2021

a) \(\left\{{}\begin{matrix}x-\sqrt{3}y=0\\\sqrt{3}x+2y=1+\sqrt{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{3}x-3y=0\\\sqrt{3}x+2y=1+\sqrt{3}\end{matrix}\right.\)

Lấy phương trình dưới trừ phương trình trên thu được: \(5y=1+\sqrt{3}\Rightarrow y=\dfrac{1+\sqrt{3}}{5}\Rightarrow x=\sqrt{3}y=\dfrac{3+\sqrt{3}}{5}\)

b) Cộng hai phương trình lại với nhau thu được:

\(\left(\sqrt{2}+1\right)x=\sqrt{2}+1\Leftrightarrow x=1\Rightarrow y=\dfrac{\sqrt{2}-1}{\sqrt{5}}\)

c) \(\left\{{}\begin{matrix}\sqrt{2}x+\sqrt{5}y=2\\x+\sqrt{5}y=2\end{matrix}\right.\)

Lấy phương trình trên trừ phương trình dưới:

\(\left(\sqrt{2}-1\right)x=0\Leftrightarrow x=0\Rightarrow y=\dfrac{2-x}{\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)

d) Hướng dẫn. Nhân phương trình đầu với \(\sqrt{2}\) rồi lấy phương trình thu được trừ phương trình dưới.

Đúng(1)
T
tthnew
18 tháng 1 2021

Sorry bạn, mình không nhìn kỹ đề nên nhầm phương pháp.

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP