TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 1 2019
Giả sử \(2x^2+ax-4\)chia cho x + 4 = \(Q\left(x\right)\)
\(\Rightarrow2x^2+ax-4=\left(x+4\right)Q\left(x\right)\)
Vì đẳng thức trên đúng với mọi x thuộc R
=> Với x = -4
\(\Rightarrow2\left(-4\right)^2+a\left(-4\right)-4=0\)
\(\Rightarrow32-4a-4=0\)
\(\Rightarrow28=4a\Leftrightarrow a=7\)
Các bài khác tương tự thôi
HH
18 tháng 1 2019
b/ Gọi thương của phép chia \(\left(x^3+ax^2+5x+3\right)\)cho \(\left(x^2+2x+3\right)\)là \(Q_{\left(x\right)}\)
=> \(x^3+ax^2+5x+3=\left(x^2+2x+3\right)Q_{\left(x\right)}\)
=> Q(x) có bậc 1
=> \(Q_{\left(x\right)}=bx+c\)
=> \(x^3+ax^2+5x+3=\left(x^2+2x+3\right)\left(bx+c\right)\)
=> \(x^3+ax^2+5x+3=bx^3+2bx^2+3bx+cx^2+2cx+3c\)
=> \(x^3+ax^2+5x+3=bx^3+\left(2b+c\right)x^2+\left(3b+2c\right)x+3c\)
Ta có \(\hept{\begin{cases}x^3=bx^3\\3c=3\end{cases}}\)=> \(\hept{\begin{cases}b=1\\c=1\end{cases}}\)
=> \(x^3+ax^2+5x+3=x^3+3x^2+5x+3\)
Đồng nhất hệ số => a = 3
16 tháng 8 2017
Ta có : \(\frac{x^3+ax+b}{x^2+2x-2}=\frac{\left(x^3+2x^2-2x\right)-\left(2x^2+4x-4\right)+ax+6x+b-4}{x^2+2x-2}\)
\(=\frac{x\left(x^2+2x-2\right)-2\left(x^2+2x-2\right)+ax+6x+b}{x^2+2x-2}\)\(=x-2+\frac{ax+6x+b-4}{x^2+2x-2}\)
Để \(x^3+ax+b⋮x^2+2x-2\) thì \(\frac{ax+6x+b-4}{x^2+2x-2}=0\Leftrightarrow x\left(a+6\right)+\left(b-4\right)=0\)
Đồng nhất ta được : \(\hept{\begin{cases}a+6=0\\b-4=0\end{cases}\Rightarrow\hept{\begin{cases}a=-6\\b=4\end{cases}}}\)
LM
2
NT
17 tháng 7 2018
Tham khảo nha bạn : http://lazi.vn/edu/exercise/xac-dinh-cac-hang-so-a-va-b-sao-cho-x4-ax-b-chia-het-cho-x2-4-x4-ax-bx-1-chia-het-cho-x2-1
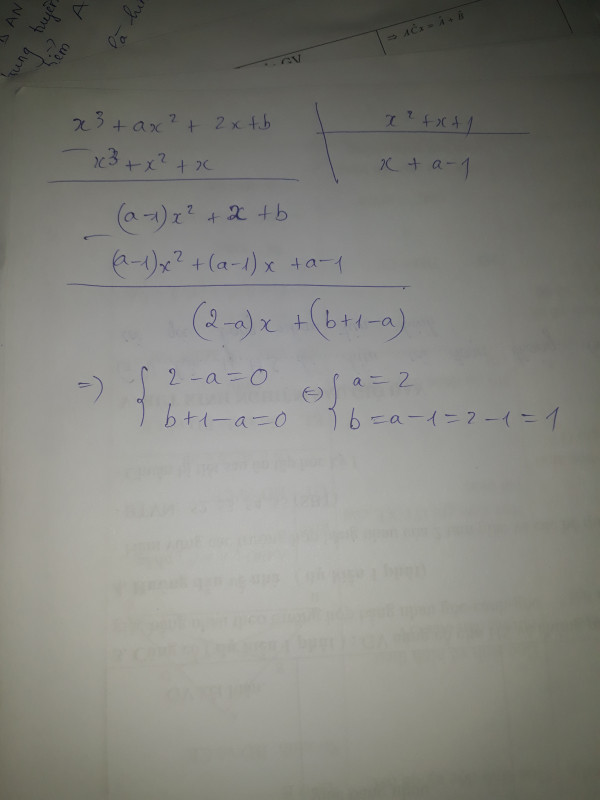
\(x^2-ax+2a-b⋮x^2+2x+1\)
nên \(\left\{{}\begin{matrix}-a=2\\2a-b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=2a-1=-5\end{matrix}\right.\)