Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(n_{Fe\left(NO_3\right)_3}=0,14mol\)
Đặt \(n_{Fe}=n_{FeO}=n_{Fe_2O_3}=n_{Fe_3O_4}=x\)
\(Fe\rightarrow Fe^{3+}\)
x x
\(FeO\rightarrow Fe^{3+}\)
x x
\(Fe_2O_3\rightarrow2Fe^{3+}\)
x 2x
\(Fe_3O_4\rightarrow3Fe^{3+}\)
x 3x
\(\Rightarrow7x=0,14\Rightarrow x=0,02\Rightarrow m=10,4g\)

Số mol H3PO4: 0,050 x 0,50 = 0,025 (mol).
H3PO4 + 3NaOH → Na3PO4 + 3H2O
1 mol 3 mol
0,025 mol 3 x 0,025 mol
Thể tích dung dịch NaOH: 0,075 lít hay 75 ml

Ta có:
Hàm \(\Psi\)được gọi là hàm chuẩn hóa nếu: \(\int\Psi.\Psi^{\circledast}d\tau=1hay\int\Psi^2d\tau=1\)
Hàm \(\Psi\)chưa chuẩn hóa là: \(\int\left|\Psi\right|^2d\tau=N\left(N\ne1\right)\)
Để có hàm chuẩn hóa, chia cả 2 vế cho N,ta có:
\(\frac{1}{N}.\int\left|\Psi\right|^2d\tau=1\Rightarrow\frac{1}{N}.\int\Psi.\Psi^{\circledast}d\tau=1\)
Trong đó: \(\Psi=\frac{1}{\sqrt{N}}.\Psi\)là hàm chuẩn hóa; \(\frac{1}{\sqrt{N}}\)là thừa số chuẩn hóa
Ta có:
\(\frac{1}{N}.\int\Psi.\Psi^{\circledast}d\tau=\frac{1}{N}.\int\left|\Psi\right|^2d\tau=1\Leftrightarrow\frac{1}{N}.\iiint\left|\Psi\right|^2dxdydz=1\)
Chuyển sang tọa độ cầu, ta có: \(\begin{cases}x=r.\cos\varphi.sin\theta\\y=r.sin\varphi.sin\theta\\z=r.\cos\theta\end{cases}\)với \(\begin{cases}0\le r\le\infty\\0\le\varphi\le2\pi\\0\le\theta\le\pi\end{cases}\)
\(\Rightarrow\frac{1}{N}.\iiint\left(r.\cos\varphi.sin\theta\right)^2.e^{-\frac{r}{a_o}}.r^2.sin\theta drd\varphi d\theta=1\)
\(\Leftrightarrow\frac{1}{N}.\int\limits^{\infty}_0r^4.e^{-\frac{r}{a_o}}dr.\int\limits^{2\pi}_0\cos^2\varphi d\varphi.\int\limits^{\pi}_0sin^3\theta d\theta=1\)
\(\Leftrightarrow\frac{1}{N}.\frac{4!}{\left(\frac{1}{a_o}\right)^5}.\int\limits^{2\pi}_0\frac{\cos\left(2\varphi\right)+1}{2}d\varphi\int\limits^{\pi}_0\frac{3.sin\theta-sin3\theta}{4}d\theta=1\)(do \(\int\limits^{\infty}_0x^n.e^{-a.x}dx=\frac{n!}{a^{n+1}}\))
\(\Leftrightarrow\frac{1}{N}.24.a^5_o.\frac{4}{3}.\pi=1\)
\(\Leftrightarrow\frac{1}{N}=\frac{1}{32.a^5_o.\pi}\)
\(\Rightarrow\)Thừa số chuẩn hóa là: \(\frac{1}{\sqrt{N}}=\sqrt{\frac{1}{32.a^5_o.\pi}}\); Hàm chuẩn hóa: \(\Psi=\frac{1}{\sqrt{N}}.\Psi=\sqrt{\frac{1}{32.a^5_o.\pi}}.x.e^{-\frac{r}{2a_o}}\)
áp dụng dk chuẩn hóa hàm sóng. \(\int\psi\psi^{\cdot}d\tau=1.\)
ta có: \(\int N.x.e^{-\frac{r}{2a_0}}.N.x.e^{-\frac{r}{2a_0}}.d\tau=1=N^2.\int_0^{\infty}r^4e^{-\frac{r}{a_0}}dr.\int_0^{\pi}\sin^3\theta d\tau.\int^{2\pi}_0\cos^2\varphi d\varphi=N^2.I_1.I_2.I_3\)
Thấy tích phân I1 có dạng tích phân hàm gamma. \(\int^{+\infty}_0x^ne^{-ax}dx=\int^{+\infty}_0\frac{\left(\left(ax\right)^{n+1-1}e^{-ax}\right)d\left(ax\right)}{a^{n+1}}=\frac{\Gamma\left(n+1\right)!}{a^{n+1}}=\frac{n!}{a^{n+1}}.\)
.áp dụng cho I1 ta được I\(I1=4!.a_0^5=24a^5_0\). tính \(I2=\int_0^{\pi}\sin^3\theta d\theta=\int_0^{\pi}\left(\cos^2-1\right)d\left(\cos\theta\right)=\frac{4}{3}\). tính tp \(I3=\int_0^{2\pi}\cos^2\varphi d\varphi=\int_0^{2\pi}\frac{\left(1-\cos\left(2\varphi\right)\right)}{2}d\varphi=\pi\)
suy ra \(\frac{N^2.24a_0^5.\pi.4}{3}=1\). vậy N=\(N=\frac{1}{\sqrt{32\pi a_0^5}}\). hàm \(\psi\) sau khi chiuẩn hóa có dạng \(\psi=\frac{1}{\sqrt{\pi32.a_0^5}}x.e^{-\frac{r}{2a_0}}\)

\(2CH_3COOH+2Na\rightarrow2CH_3COONa+H_2\uparrow\)
\(m_{CH_3COOH}=60\left(g\right)\)
\(n_{CH_3COOH}=1\left(mol\right)\)
\(\Rightarrow n_{H_2}=0,5\left(mol\right)\Rightarrow m_{H_2}=1\left(g\right)\)
2CH\(_3\)COOH+2Na\(\Leftrightarrow\)2CH\(_3\)COONa+H\(_2\uparrow\)
MCH\(_3\)COOH=60(G)
NCH\(_3\)COOH=1(MOL)
\(\Leftrightarrow\)NH\(_2\)=0,5(MOL)\(\Leftrightarrow\)MH\(_2\)=1(G)

Đáp án D
Este được tạo ra từ hai axit đơn chức, mạch hở và một ancol đơn chức
⇒ Hỗn hợp chứa 2 este no đơn chức mạch hở.
⇒ nEste = nNaOH = 0,1 mol ⇒ MHỗn hợp este = 65,6
⇒ Este bé chỉ có thể là HCOONH3.
+ Vì tạo ra cùng ancol ⇒ nAncol = nCH3OH = nNaOh = 0,1 mol.
⇒ mCH3OH = 3,2 gam.
+ Bảo toàn khối lượng ta có: mMuối = 6,56 + 0,1×40 – 3,2 = 7,36 gam
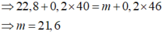 .
.
Chọn A