
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(bn\)\(xem\)\(lai\)\(giup\)\(mk\)\(cho\)\(\frac{x+522}{7}\)\(neu\)\(thay\)\(bang\)\(\frac{x+552}{7}\)\(thi\)\(dug\)\(hon\)
thế thì bạn giải thử xem cô t ra đề thế mà ừ thì cứ cho là x + 552 cx đc

. Số nào trong các số sau đây viết được dưới dạng số thập phân hữu hạn?
A. 521 B. 56 C. - 435 D. 2724


O B A C O'
Lấy điểm O' sao cho \(OB\perp O'B;OB=O'B\)( O' cùng phía với C so với OB)=> O' cố định
Khi đó góc OBA = Góc O'BC( cùng phụ góc ABO')
=> \(\Delta BOA=\Delta BO'C\)( cạnh.góc.canh)
=> \(O'C=OA=1\)
Mà O' cố định
=> C thuộc đường tròn tâm O' BK=1 cố định
Để OC lớn nhất thì
C là giao của OO' với đường tròn tâm O' (C nằm ngoài OO')
ÁP dụng PItago ta có \(OO'=\sqrt{2}\)
=> \(OC=OO'+O'C=1+\sqrt{2}\)
Vậy \(MaxOC=1+\sqrt{2}\)
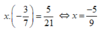
`-x-521=-17363`
`=>-x=-17363+521`
`=>-x=-16842`
`=>x=16842`
-x=-17363+521
-x=-16842
x=16842