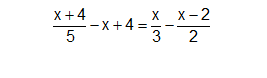Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta=4+4.7=32\)
\(\orbr{\begin{cases}x_1=\frac{-2+4\sqrt{2}}{2}=-1+2\sqrt{2}\\x_2=\frac{-2-4\sqrt{2}}{2}=-1-2\sqrt{2}\end{cases}}\)

\(\left|-2x\right|-3x=4\)
\(\Leftrightarrow\left|-2x\right|=4+3x\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=4+3x\\-2x=-\left(4+3x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x-3x=4\\-2x=-4-3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-5x=4\\-2x+3x=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{5}\\x=-4\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{4}{5};-4\right\}\)

\(H=3x-5-3x^2\)
\(=-3\left(x^2-x+\frac{5}{3}\right)\)
\(=-3\left(x^2-2.x.\frac{1}{2}+\frac{1}{4}+\frac{17}{12}\right)\)
\(=-3\left(\left(x-\frac{1}{2}\right)^2+\frac{17}{12}\right)\)
\(=\frac{-17}{4}-3\left(x-\frac{1}{2}\right)^2\le\frac{-17}{4}\)
\(MAXH=\frac{-17}{4}\Leftrightarrow x-\frac{1}{2}=0\Rightarrow x=\frac{1}{2}\)

\(\dfrac{x+4}{5}-x+4=\dfrac{x}{3}-\dfrac{x-2}{2}\)\(\Leftrightarrow\)\(\dfrac{x+4}{5}-\dfrac{5x}{5}+\dfrac{20}{5}=\dfrac{2x}{6}-\dfrac{3\left(x-2\right)}{6}\)
\(\Leftrightarrow\)\(\dfrac{-4x+24}{5}=\dfrac{-x+6}{6}\Leftrightarrow6\cdot\left(-4x+24\right)=5\cdot\left(-x+6\right)\)
\(\Leftrightarrow\)-24x+144=-5x+30\(\Leftrightarrow\)-24x+5x=30-144\(\Leftrightarrow\)-19x=-114\(\Leftrightarrow\)x=6

\(\Leftrightarrow2x^2+10x-x^2+6x-9=x^2+6\)
=>16x-9=6
=>16x=15
hay x=15/16
\(PT\Leftrightarrow2x^2+10x-x^2+6x-9-x^2-6=0.\)
\(\Leftrightarrow16x-15=0.\\ \Leftrightarrow x=\dfrac{15}{16}.\)


Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)

a, Thay x = 2 ta được 6 - 5 = 3 - 2 (luondung)
Vậy x = 2 là nghiệm pt trên
Thay x = 1 ta được 3 - 5 = 3 - 1 (voli)
Vậy x = 1 ko phải là nghiệm pt trên
b, Thay x = 2 ta được \(2m=m+6\Leftrightarrow m=6\)