A
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LG
2
XO
1 tháng 10 2020
Ta có :\(\frac{x+4}{2018}+\frac{x+3}{2019}=\frac{x+2}{2020}+\frac{x+1}{2021}\)
=> \(\left(\frac{x+4}{2018}+1\right)+\left(\frac{x+3}{2019}+1\right)=\left(\frac{x+2}{2020}+1\right)+\left(\frac{x+1}{2021}+1\right)\)
=> \(\frac{x+2022}{2018}+\frac{x+2022}{2019}=\frac{x+2022}{2020}+\frac{x+2022}{2021}\)
=> \(\frac{x+2022}{2018}+\frac{x+2022}{2019}-\frac{x+2022}{2020}-\frac{x+2022}{2021}=0\)
=> \(\left(x+2022\right)\left(\frac{1}{2018}+\frac{1}{2019}-\frac{1}{2020}-\frac{1}{2021}\right)=0\)
Vì \(\frac{1}{2018}+\frac{1}{2019}-\frac{1}{2020}-\frac{1}{2021}\ne0\)
=> x + 2022 = 0
=> x = -2022
Vậy x = -2022
1 tháng 10 2020
\(\frac{x+4}{2018}+\frac{x+3}{2019}=\frac{x+2}{2020}+\frac{x+1}{2021}\)
\(\frac{x+4}{2018}+1+\frac{x+3}{2019}+1=\frac{x+2}{2020}+1+\frac{x+1}{2021}+1\)
\(\frac{x+4}{2018}+\frac{2018}{2018}+\frac{x+3}{2019}+\frac{2019}{2019}=\frac{x+2}{2020}+\frac{2020}{2020}+\frac{x+1}{2021}+\frac{2021}{2021}\)
\(\frac{x+2022}{2018}+\frac{x+2022}{2019}=\frac{x+2022}{2020}+\frac{x+2022}{2021}\)
\(\frac{x+2022}{2018}+\frac{x+2022}{2019}-\frac{x+2022}{2020}-\frac{x+2022}{2021}=0\)
\(\left(x+2022\right)\left(\frac{1}{2018}+\frac{1}{2019}-\frac{1}{2020}-\frac{1}{2021}\right)=0\)
\(x+2022=0\left(\frac{1}{2018}+\frac{1}{2019}-\frac{1}{2020}-\frac{1}{2021}\ne0\right)\)
\(x=0-2022\)
\(x=-2022\)
HD
2
7 tháng 10 2020
\(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+...+\frac{1}{x\cdot\left(x+1\right)}=\frac{2020}{2021}\)
\(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{x}-\frac{1}{x+1}=\frac{2020}{2021}\)
\\(1-\frac{1}{x+1}=\frac{2020}{2021}\)
\(\frac{1}{x+1}=1-\frac{2020}{2021}\)
\(\frac{1}{x+1}=\frac{1}{2021}\)
\(\Rightarrow x+1=2021\)
\(x=2021-1\)
\(x=2020\)
7 tháng 10 2020
đk: \(x\ne\left\{0;-1\right\}\)
Ta có: \(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{x\left(x+1\right)}=\frac{2020}{2021}\)
\(\Leftrightarrow1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{x}-\frac{1}{x+1}=\frac{2020}{2021}\)
\(\Leftrightarrow1-\frac{1}{x+1}=\frac{2020}{2021}\)
\(\Leftrightarrow\frac{x}{x+1}=\frac{2020}{2021}\)
\(\Leftrightarrow2021x=2020x+2020\)
\(\Rightarrow x=2020\)
LD
30 tháng 10 2021
Ta có:
\(\frac{xy}{x+y}=\frac{yz}{y+z}=\frac{zx}{z+x}\rightarrow\frac{x+y}{xy}=\frac{y+z}{yz}=\frac{z+x}{zx}\)
\(\Rightarrow\frac{1}{x}+\frac{1}{y}=\frac{1}{y}+\frac{1}{z}=\frac{1}{z}+\frac{1}{x}\Rightarrow\frac{1}{x}=\frac{1}{y}=\frac{1}{z}\Rightarrow x=y=z\)
Thay tất cả giá trị x,y,z vào M ta được:
\(M=\frac{2020x^3+2020y^3+2020z^3}{x^3+y^3+z^3}+\frac{2021x^5+2021y^5}{x^5+y^5}\)
\(\Rightarrow M=\frac{2020\left(x^3+y^3+z^3\right)}{x^3+y^3+z^3}+\frac{2021\left(x^5+y^5\right)}{x^5+y^5}\)
\(\Rightarrow M=2020+2021=4041\)
NM
2
CN
1 tháng 1 2018
\(\dfrac{x-4}{2021}+\dfrac{x-3}{2020}=\dfrac{x-2}{2019}+\dfrac{x-1}{2018}\)
⇔ \(\dfrac{x-4}{2021}+\dfrac{x-3}{2020}-\dfrac{x-2}{2019}-\dfrac{x-1}{2018}=0\)
⇔ \(\left(1+\dfrac{x-4}{2021}\right)+\left(1+\dfrac{x-3}{2020}\right)-\left(1+\dfrac{x-2}{2019}\right)-\left(1+\dfrac{x-1}{2018}\right)=0\)⇔ \(\dfrac{x+2017}{2021}+\dfrac{x+2017}{2020}-\dfrac{x+2017}{2019}-\dfrac{x+2017}{2018}=0\)
⇔ \(\left(x+2017\right)\left(\dfrac{1}{2021}+\dfrac{1}{2020}-\dfrac{1}{2019}-\dfrac{1}{2018}\right)=0\)
⇔ x + 2017 = 0
⇔ x = -2017
Vậy x = -2017
CT
3
I
5 tháng 1 2023
\(\dfrac{x+1}{2023}+\dfrac{x+2}{2022}=\dfrac{x+3}{2021}+\dfrac{x+4}{2020}\\ \Leftrightarrow\dfrac{x+1}{2023}+1+\dfrac{x+2}{2022}+1=\dfrac{x+3}{2021}+1+\dfrac{x+4}{2020}+1\\ \Leftrightarrow\dfrac{x+1+2023}{2023}+\dfrac{x+2+2022}{2022}-\dfrac{x+3+2021}{2021}-\dfrac{x+4+2020}{2020}=0\\ \Leftrightarrow\left(x+2024\right)\times\left(\dfrac{1}{2023}+\dfrac{1}{2022}-\dfrac{1}{2021}-\dfrac{1}{2020}\right)=0\\ \Rightarrow x+2024=0:\left(\dfrac{1}{2023}+\dfrac{1}{2022}-\dfrac{1}{2021}-\dfrac{1}{2020}\right)\\ \Rightarrow x+2024=0\\ \Rightarrow x=-2024\)
6 tháng 5 2021
a)
P(x) + O(x) = \(\left(x^3+2x^2-3x+2020\right)+\left(2x^3-3x^2+4x+2021\right)\)
P(x) + O(x) = \(3x^3-x^2+x+4041\)
b)
P(x) - O(x) = \(x^3+2x^2-3x+2020-2x^3+3x^2-4x-2021\)
P(x) - O(x) = \(-x^3+5x^2-7x-1\)
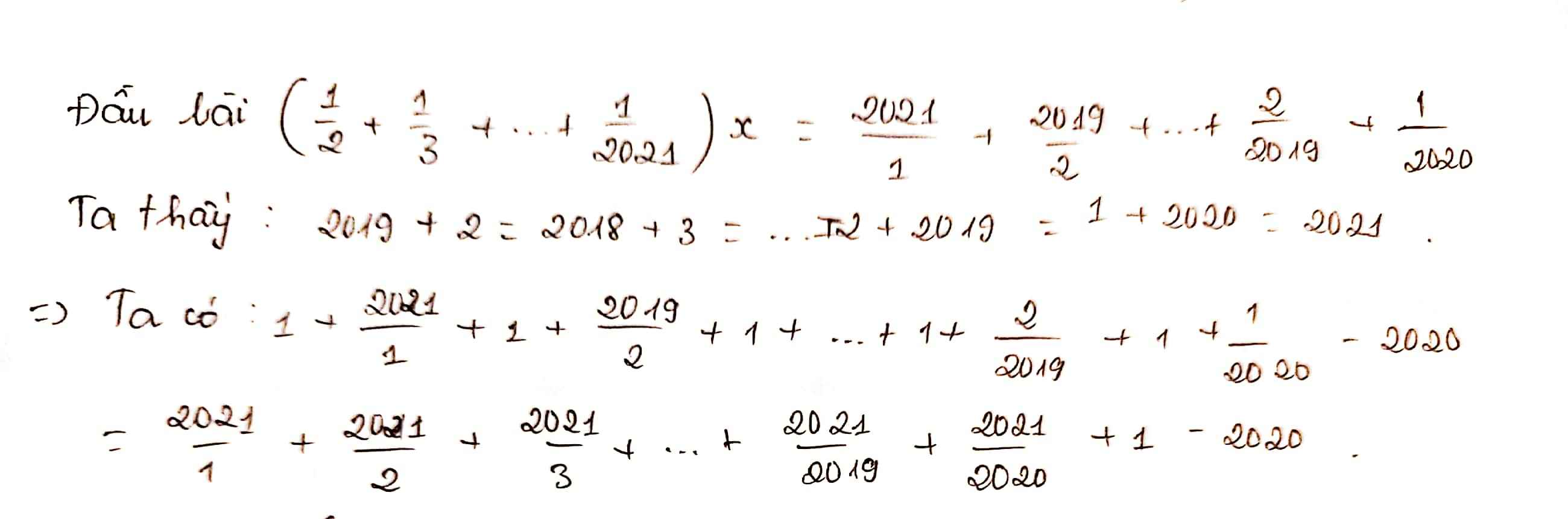
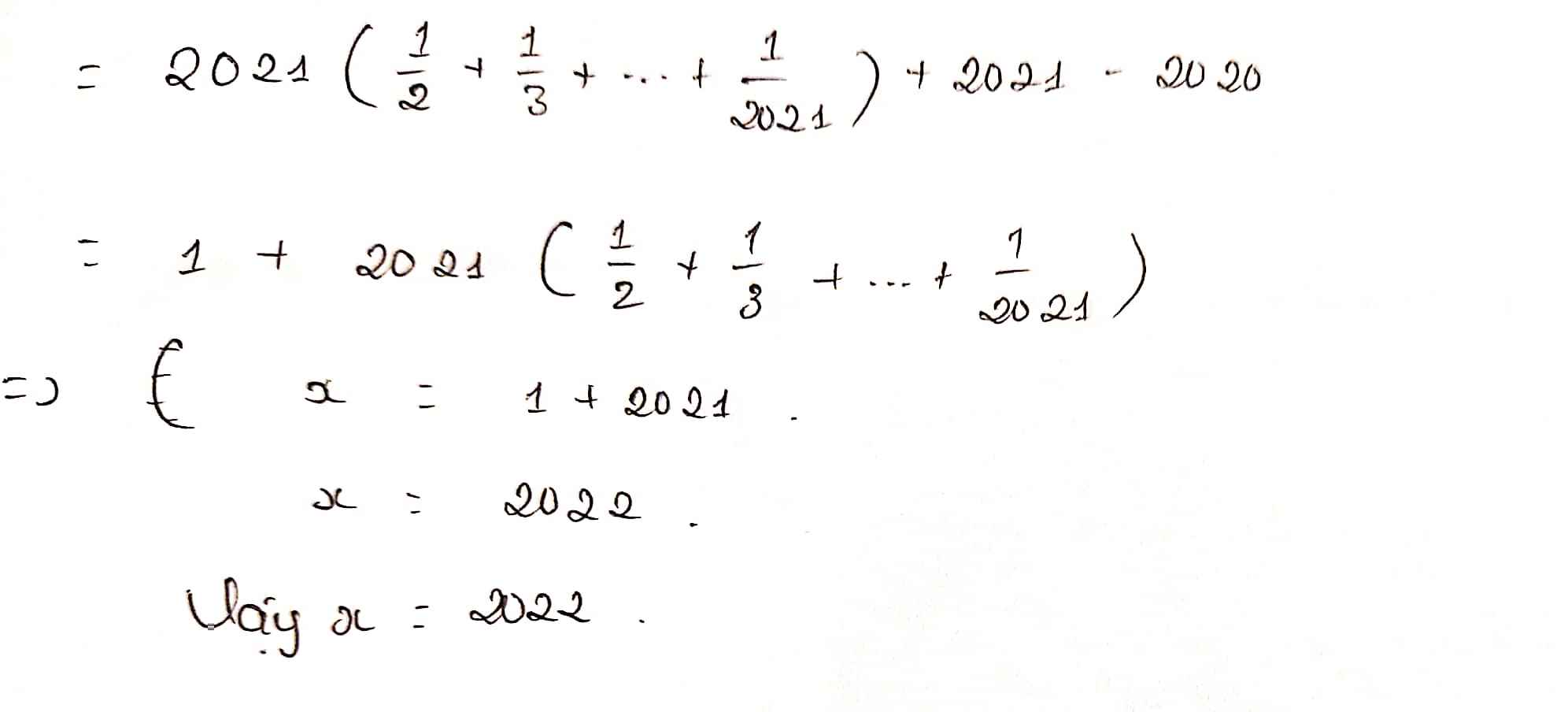
có sai đề ko bn