Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\left\{{}\begin{matrix}x_1+x_2=8\\x_1x_2=6\end{matrix}\right.\)
\(D=x_1^4-x_2^4=\left(x_1+x_2\right)\left(x_1-x_2\right)\left(x_1^2+x_2^2\right)\)
\(=8\cdot\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\cdot\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=8\cdot\left[8^2-2\cdot6\right]\cdot\sqrt{8^2-4\cdot6}\)
\(=8\cdot52\cdot2\sqrt{10}=832\sqrt{10}\)
b: \(E=\left(x_1^2+x_2^2\right)^2-2x_1^2\cdot x_2^2\)
\(=52^2-2\cdot\left(x_1\cdot x_2\right)^2=52^2-2\cdot6^2=2632\)
c: \(F=\dfrac{3x_2^2+3x_1^2}{\left(x_1\cdot x_2\right)^2}=\dfrac{3\cdot52}{6^2}=\dfrac{13}{3}\)

\(-x^2+2\left(2+m\right)x-m^2=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(2+m\right)\\x_1x_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
Ta có :
\(\left|x_1+x_2-4\right|=2x_1x_2\)
\(\Leftrightarrow\left|4+2m-4\right|=2m^2\)
\(\Leftrightarrow\left|2m\right|=2m^2\)
\(\Leftrightarrow\left[{}\begin{matrix}2m=2m^2\\2m=-2m^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2m-2m^2=0\\2m+2m^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2m\left(1-m\right)=0\\2m\left(1+m\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=1\\m=-1\end{matrix}\right.\)


8.1/ Để phương trình có 2 nghiệm phân biệt thì \(\Delta=\left(m-9\right)^2-4.\left(-7\right)=m^2-18m+109>0\Leftrightarrow m\in R\)
Theo định lý viete, ta có: \(\left\{{}\begin{matrix}x_1+x_2=m+9\\x_1x_2=-7< 0\end{matrix}\right.\)
\(\left|x_1\right|-\left|x_2\right|=16\Leftrightarrow x_1^2+x_2^2-2\left|x_1x_2\right|=256\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|=256\Leftrightarrow\left(m+9\right)^2=256-2\left(-7\right)-2\left|-7\right|=256\)
\(\Leftrightarrow\left(m+9\right)^2=256\Leftrightarrow\left[{}\begin{matrix}m=7\\m=-25\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=7\\m=-25\end{matrix}\right.\)
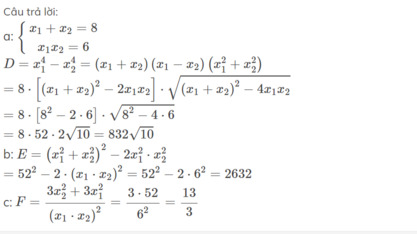

\(x^2+1-12=0\)
Theo Vi - ét , ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=0\\x_1x_2=\dfrac{c}{a}=-11\end{matrix}\right.\)
Ta có :
\(A=x_1^2+x_2^2+x_1^2x_2+x_1x^2_2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2+x_1x_2\left(x_1+x_2\right)\)
\(=0^2-2\left(-11\right)-11\left(0\right)\)
\(=22-11\)
\(=11\)
Vậy \(A=11\)
Bạn xem lại giúp mình pt \(x^2+1-12=0\) có thiếu \(x\) không vậy ?