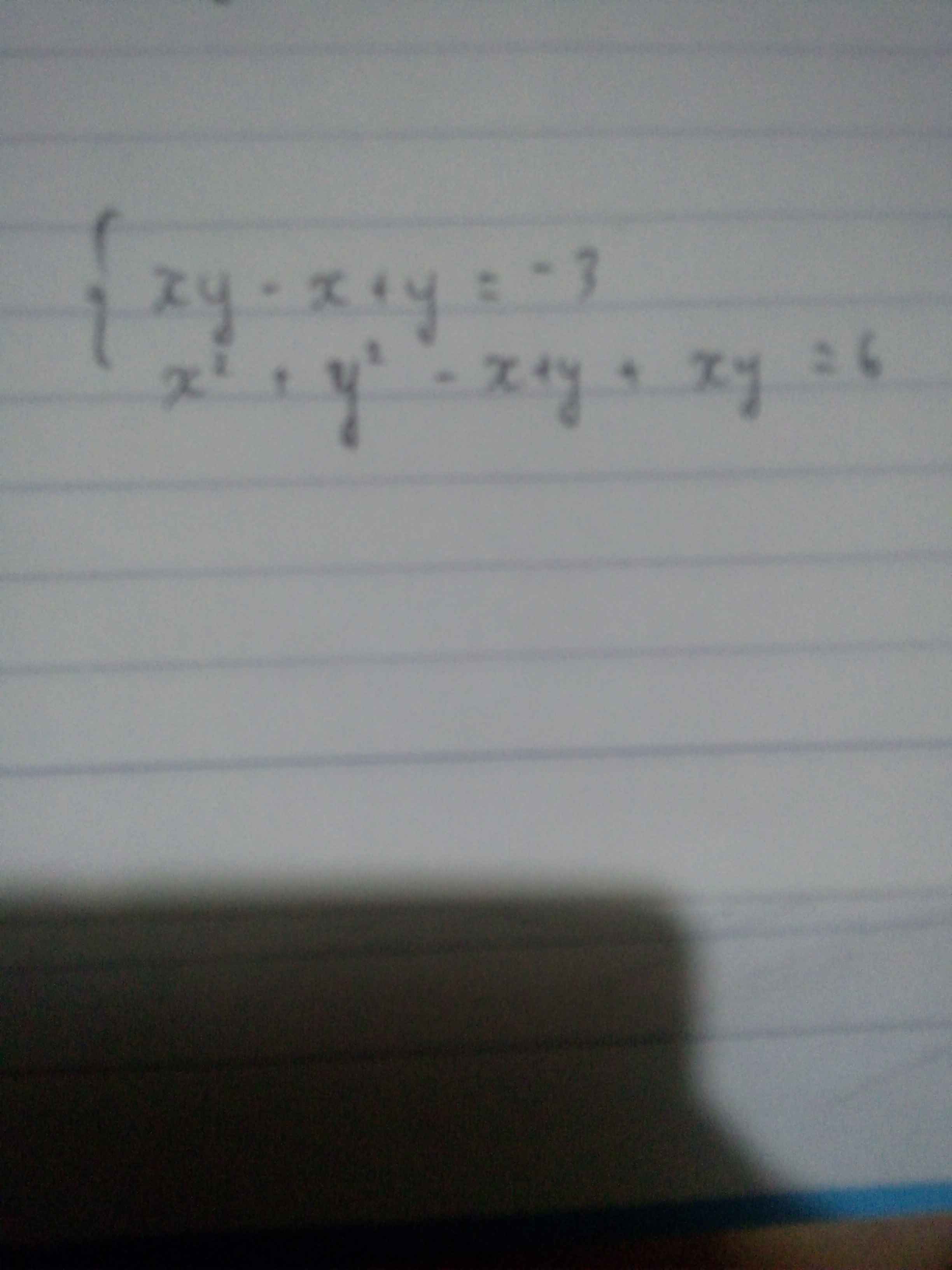Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left\{{}\begin{matrix}3xy-3\left(x-y\right)=-9\\x^2+y^2+xy-\left(x-y\right)=6\end{matrix}\right.\)
Trừ vế cho vế:
\(x^2+y^2-2xy+2\left(x-y\right)=15\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)-15=0\Rightarrow\left[{}\begin{matrix}x-y=3\\x-y=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=x-3\\y=x+5\end{matrix}\right.\)
Thế vào pt đầu:
\(\Rightarrow\left[{}\begin{matrix}x\left(x-3\right)-x+x-3=-3\\x\left(x+5\right)-x+x+5=-3\end{matrix}\right.\)
\(\Leftrightarrow...\)

Lời giải:
\(D=\frac{x}{y}+\frac{y}{x}+\frac{xy}{x^2+xy+y^2}=\frac{x^2+y^2}{xy}+\frac{xy}{x^2+xy+y^2}\)
\(=\frac{x^2+xy+y^2}{xy}+\frac{xy}{x^2+xy+y^2}-1\)
\(\frac{x^2+xy+y^2}{9xy}+\frac{xy}{x^2+xy+y^2}+\frac{8(x^2+xy+y^2)}{9xy}-1\)
Áp dụng BĐT Cô-si:
\(\frac{x^2+xy+y^2}{9xy}+\frac{xy}{x^2+xy+y^2}\geq 2\sqrt{\frac{x^2+xy+y^2}{9xy}.\frac{xy}{x^2+xy+y^2}}=\frac{2}{3}\)
\(x^2+y^2\geq 2xy\Rightarrow \frac{8(x^2+xy+y^2)}{9xy}\geq \frac{8.3xy}{9xy}=\frac{8}{3}\)
\(\Rightarrow D\geq \frac{2}{3}+\frac{8}{3}-1=\frac{7}{3}=D_{\min}\)
Dấu "=" xảy ra khi $x=y$