
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100=10^2\)
=>BC=10(cm)
Xét ΔABC vuông tại A có \(\sin C=\frac{AB}{BC}=\frac{6}{10}=\frac35\)
nên \(\hat{C}\) ≃37 độ
ΔABC vuông tại A
=>\(\hat{B}+\hat{C}=90^0\)
=>\(\hat{B}=90^0-37^0=53^0\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(1\right)\)
Xét ΔABD vuông tại A có AK là đường cao
nên \(BK\cdot BD=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BH\cdot BC=BK\cdot BD\)
c: \(BH\cdot BC=BD\cdot BK\)
=>\(\frac{BH}{BK}=\frac{BD}{BC}\)
=>\(\frac{BH}{BD}=\frac{BK}{BC}\)
Xét ΔBHK và ΔBDC có
\(\frac{BH}{BD}=\frac{BK}{BC}\)
góc HBK chung
Do đó: ΔBHK~ΔBDC
=>\(\hat{BKH}=\hat{BCD}=\hat{ACB}\)

a: ta có: AH⊥CD
OM⊥CD
BK⊥CD
Do đó: AH//OM//BK
Xét ΔAKB có
O là trung điểm của AB
ON//KB
DO đó: N là trung điểm của AK
=>AN=NK
b: Xét hình thang ABKH có
O là trung điểm của AB
OM//AH//BK
Do đó: M là trung điểm của HK
=>MH=MK
c: ΔOCD cân tại O
mà OM là đường cao
nên M là trung điểm của CD
Ta có: MC+CH=MH
MD+DK=MK
mà MC=MD và MH=MK
nên CH=DK

Bài 4:
a: ΔCAB vuông tại C
=>\(\hat{CAB}+\hat{CBA}=90^0\)
=>\(\hat{CBA}=90^0-70^0=20^0\)
Xét ΔCBA vuông tại C có \(\sin CBA=\frac{CA}{AB}\)
=>\(CA=AB\cdot\sin CBA=10\cdot\sin20\) ≃3,4(dm)
ΔCAB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(CB^2=AB^2-CA^2\)
=>\(CB=\sqrt{AB^2-AC^2}\) ≃9,4(dm)
b: Xét ΔABC vuông tại C có \(cosA=\frac{CA}{AB}\)
Xét ΔCHA vuông tại H có \(cosA=\frac{AH}{AC}\)
Xét ΔCHB vuông tại H có \(\sin B=\frac{CH}{CB}\)
Xét ΔCAB vuông tại C có \(\sin B=\frac{AC}{AB}\)
\(\sin B\cdot cosA=\frac{AC}{AB}\cdot\frac{AH}{AC}=\frac{AH}{AB}\)
Bài 5:
Xét ΔMAB có \(\hat{MBH}\) là góc ngoài tại đỉnh B
nên \(\hat{MBH}=\hat{A}+\hat{BMA}\)
=>\(\hat{BMA}=39^0-18^0=21^0\)
Xét ΔMAB có \(\frac{AB}{\sin AMB}=\frac{MB}{\sin A}\)
=>\(\frac{MB}{\sin18}=\frac{80}{\sin21}\)
=>\(MB=80\cdot\frac{\sin18}{\sin21}\) ≃69(m)
Xét ΔMHB vuông tại H có \(\sin HBM=\frac{HM}{MB}\)
=>\(HM=MB\cdot\sin HBM\) ≃69*sin39≃43,4(m)
=>Chiều cao của ngọn hải đăng là khoảng 43,4 mét

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64=8^2\)
=>AC=8(cm)
Xét ΔABC vuông tại A có \(\sin C=\frac{AB}{BC}=\frac{6}{10}=\frac35\)
nên \(\hat{C}\) ≃37 độ
ΔABC vuông tại A
=>\(\hat{B}+\hat{C}=90^0\)
=>\(\hat{B}=90^0-37^0=53^0\)
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\) (2)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
\(AE\cdot AB=AH^2\)
=>\(AE=\frac{AH^2}{AB}\)
\(AF\cdot AC=AH^2\)
=>\(AF=\frac{AH^2}{AC}\)
Xét tứ giác AEHF có \(\hat{AEH}=\hat{AFH}=\hat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>\(S_{AEHF}=AE\cdot AF=\frac{AH^2}{AB}\cdot\frac{AH^2}{AC}=\frac{AH^4}{AH\cdot BC}=\frac{AH^3}{BC}\)

Bài 3:
a: ΔOBC cân tại O
mà OI là đường cao
nên I là trung điểm của BC
Xét ΔBOD có
BI là đường cao
BI là đường trung tuyến
Do đó: ΔBOD cân tại B
=>BO=BD
ma BO=OD
nên BO=BD=OD
=>ΔBOD đều
=>\(\hat{BOD}=\hat{BDO}=\hat{OBD}=60^0\)
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>\(\hat{BAD}+\hat{BDA}=90^0\)
=>\(\hat{BAD}=90^0-60^0=30^0\)
Xét ΔAIB vuông tại I và ΔAIC vuông tại I có
AI chung
IB=IC
Do đó: ΔAIB=ΔAIC
=>AB=AC
ΔAIB=ΔAIC
=>\(\hat{IAB}=\hat{IAC}\)
=>AI là phân giác của góc BAC
=>\(\hat{BAC}=2\cdot\hat{BAD}=2\cdot30^0=60^0\)
Xét ΔABC có AB=AC và \(\hat{BAC}=60^0\)
nên ΔABC đều
b: ΔOBD đều
=>BD=OB=R
ΔABD vuông tại B
=>\(BA^2+BD^2=AD^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt3\)
=>\(BA=AC=BC=R\sqrt3\)
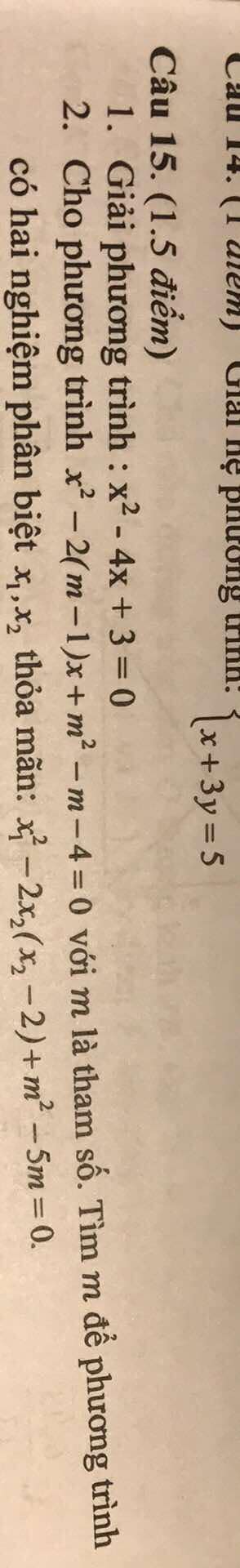







Câu 1:
x2−4x+3=0x^2 - 4x + 3 = 0x2−4x+3=0
Phương trình này là phương trình bậc hai có dạng chuẩn ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0 với:
Tính biệt số Δ\DeltaΔ:
Δ=b2−4ac=(−4)2−4(1)(3)=16−12=4.\Delta = b^2 - 4ac = (-4)^2 - 4(1)(3) = 16 - 12 = 4.Δ=b2−4ac=(−4)2−4(1)(3)=16−12=4.
Vì Δ>0\Delta > 0Δ>0, phương trình có hai nghiệm phân biệt:
x=−b±Δ2a=4±22.x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{4 \pm 2}{2}.x=2a−b±Δ=24±2.
Suy ra hai nghiệm:
x1=4−22=1,x2=4+22=3.x_1 = \frac{4 - 2}{2} = 1, \quad x_2 = \frac{4 + 2}{2} = 3.x1=24−2=1,x2=24+2=3.
Vậy nghiệm của phương trình là x=1x = 1x=1 hoặc x=3x = 3x=3.
Câu 2
Phương trình:
x2−2(m−1)x+m2−m−4=0x^2 - 2(m-1)x + m^2 - m - 4 = 0x2−2(m−1)x+m2−m−4=0
Có hai nghiệm phân biệt khi:
Δ′=(m−1)2−(m2−m−4)>0.\Delta' = (m-1)^2 - (m^2 - m - 4) > 0.Δ′=(m−1)2−(m2−m−4)>0.
Tính toán:
m2−2m+1−m2+m+4>0.m^2 - 2m + 1 - m^2 + m + 4 > 0.m2−2m+1−m2+m+4>0. −m+5>0.- m + 5 > 0.−m+5>0. m<5.m < 5.m<5.
Ta có điều kiện:
x12−2x2(x2−2)+m2−5m=0.x_1^2 - 2x_2(x_2 - 2) + m^2 - 5m = 0.x12−2x2(x2−2)+m2−5m=0.
Sử dụng định lý Vi-ét
x1+x2=2(m−1),x_1 + x_2 = 2(m-1),x1+x2=2(m−1), x1x2=m2−m−4.x_1 x_2 = m^2 - m - 4.x1x2=m2−m−4.
Dùng đẳng thức:
x12=(x1+x2)2−2x1x2.x_1^2 = (x_1 + x_2)^2 - 2x_1 x_2.x12=(x1+x2)2−2x1x2.
Thay vào:
(2(m−1))2−2(m2−m−4)−2x2(x2−2)+m2−5m=0.(2(m-1))^2 - 2(m^2 - m - 4) - 2x_2(x_2 - 2) + m^2 - 5m = 0.(2(m−1))2−2(m2−m−4)−2x2(x2−2)+m2−5m=0.
Biến đổi:
4(m−1)2−2(m2−m−4)−2x22+4x2+m2−5m=0.4(m-1)^2 - 2(m^2 - m - 4) - 2x_2^2 + 4x_2 + m^2 - 5m = 0.4(m−1)2−2(m2−m−4)−2x22+4x2+m2−5m=0.
Dùng x22=(x1+x2)2−2x1x2x_2^2 = (x_1 + x_2)^2 - 2x_1x_2x22=(x1+x2)2−2x1x2, thay vào:
4(m−1)2−2(m2−m−4)−2[(2(m−1))2−2(m2−m−4)]+4x2+m2−5m=0.4(m-1)^2 - 2(m^2 - m - 4) - 2[(2(m-1))^2 - 2(m^2 - m - 4)] + 4x_2 + m^2 - 5m = 0.4(m−1)2−2(m2−m−4)−2[(2(m−1))2−2(m2−m−4)]+4x2+m2−5m=0.
Rút gọn:
4(m2−2m+1)−2m2+2m+8−2[4(m2−2m+1)−2m2+2m+8]+4x2+m2−5m=0.4(m^2 - 2m + 1) - 2m^2 + 2m + 8 - 2[4(m^2 - 2m + 1) - 2m^2 + 2m + 8] + 4x_2 + m^2 - 5m = 0.4(m2−2m+1)−2m2+2m+8−2[4(m2−2m+1)−2m2+2m+8]+4x2+m2−5m=0.
Sau khi tiếp tục biến đổi và rút gọn, ta giải phương trình để tìm các giá trị mmm thỏa mãn.
Kết quả cuối cùng là m=3m = 3m=3 (thỏa mãn cả hai điều kiện trên).