PN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MT
9 tháng 7 2015
(2x^2-3x+1) (x^2-5)-(x^2-x) (2x^2-x-10)=5
<=>2x4-3x3+x2-10x2+15x-5-(2x4-x3-10x2-2x3+x2+10x)=5
<=>2x4-3x3+x2-10x2+15x-5-2x4+x3+10x2+2x3-x2-10x=5
<=>5x-5=5
<=>5x=10
<=>x=2
H9
HT.Phong (9A5)
CTVHS
2 tháng 10 2023
Ta có: \(C=\dfrac{2x+1}{x^2+x-2}=\dfrac{2x+1}{\left(x-1\right)\left(x+2\right)}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne1\\x\ne-2\end{matrix}\right.\)
\(\left|2x+5\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+5=7\left(x\ge-\dfrac{5}{2}\right)\\2x+5=-7\left(x< -\dfrac{5}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-12\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(ktm\right)\\x=-6\left(tm\right)\end{matrix}\right.\)
Thay x=-6 vào C ta có:
\(C=\dfrac{2\cdot-6+1}{\left(-6\right)^2+\left(-6\right)-2}=\dfrac{-12+1}{36-6-2}=\dfrac{-11}{28}\)
DL
5 tháng 10 2019
a, ĐKXĐ: \(\hept{\begin{cases}x^3+1\ne0\\x^9+x^7-3x^2-3\ne0\\x^2+1\ne0\end{cases}}\)
b, \(Q=\left[\left(x^4-x+\frac{x-3}{x^3+1}\right).\frac{\left(x^3-2x^2+2x-1\right)\left(x+1\right)}{x^9+x^7-3x^2-3}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)
\(Q=\left[\frac{\left(x^3+1\right)\left(x^4-x\right)+x-3}{\left(x+1\right)\left(x^2-x+1\right)}.\frac{\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)}{\left(x^7-3\right)\left(x^2+1\right)}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)
\(Q=\left[\left(x^7-3\right).\frac{\left(x-1\right)}{\left(x^7-3\right)\left(x^2+1\right)}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)
\(Q=\frac{x-1+x^2+1-2x-12}{x^2+1}\)
\(Q=\frac{\left(x-4\right)\left(x+3\right)}{x^2+1}\)
PT
3
13 tháng 9 2018
(3x-5)^2 - (3x+1)^2 =8
(3x)^2 - 2*3x*5 + 5^2 -[(3x)^2 + 2*3x*5 + 1^2]= 8
9x^2 - 30x + 25 - (9x^2 + 30x + 1) = 8
9x^2 - 30x + 25 - 9x^2 - 30x - 1 = 8
- 30x + 25 - 30x - 1 = 8
2*(-30x) + (25 - 1) = 8
-60x + 24 = 8
-60x = 8 - 24
-60x = -16
x = -16 / -60
x = 16 / 60
x = 16 * 1/60
x = 16/60
x = 4/15
DT
1
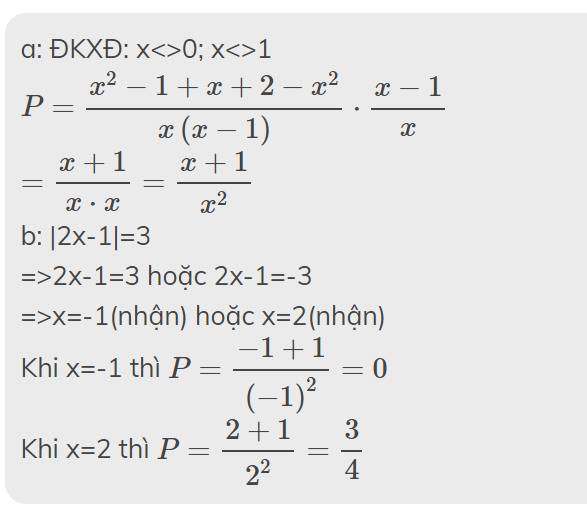
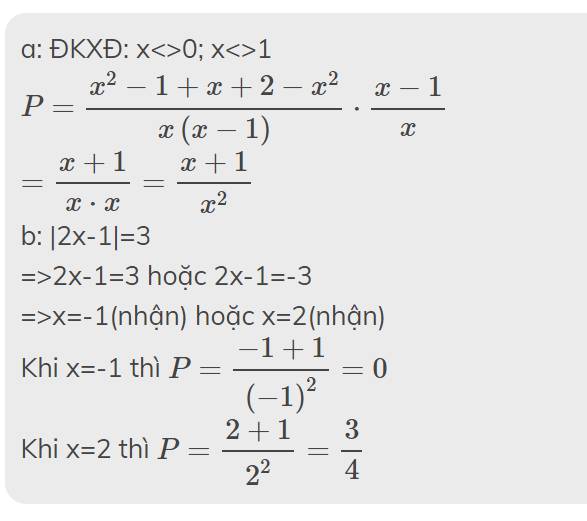
(x^2-2x+5) (x-2)=(x^2+x) (x-5).
<=>x3-2x2+5x-2x2+4x-10=x3+x2-5x2-5x
<=>x3-4x2+9x-10=x3-4x2-5x
<=>x3-4x2+9x-x3+4x2+5x=10
<=>14x=10
<=>x=5/7