
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


#\(N\)
`a,` Xét Tam giác `MPH` và Tam giác `MQH` có:
`MP = MQ (g``t)`
`MH` chung
\(\widehat{MHP}=\widehat{MHQ}=90^0\)
`=>` Tam giác `MPH =` Tam giác `MQH (ch - cgv)`
`=>`\(\widehat{MPH}=\widehat{MQH}\) `( 2` góc tương ứng `)`
`b,` Vì Tam giác `MPH =` Tam giác `MQH (a)`
`=>` \(\widehat{PMH}=\widehat{QMH}\) `( 2` góc tương ứng `)`
`=> MH` là tia phân giác của \(\widehat{PMQ}\)
`c,` Ta có: \(\widehat{MPH}=\widehat{MQH}=50^0\) `(CMT)`
Xét Tam giác `MQH` có:
\(\widehat{MHQ}+\widehat{MQH}+\widehat{QMH}=180^0\) `(`đlí tổng `3` góc trong `1` tam giác `)`
\(90^0+50^0+\widehat{QMH}=180^0\)
`->`\(\widehat{QMH}=180^0-90^0-50^0=40^0\)

Bài 1:
Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
KA=KH
=>ΔBAK=ΔBHK
=>BA=BH
mà KA=KH
nên BK là trung trực của AH
=>BK vuông góc AH

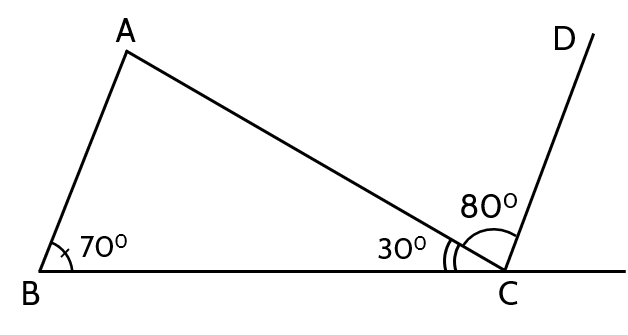
Xét tg ABC có
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}\) (tổng các góc trong của 1 tg \(=180^o\) )
\(\Rightarrow\widehat{BAC}=180^o-70^o-30^o=80^o=\widehat{ACD}\)
Hai góc \(\widehat{BAC}=\widehat{ACD}\) ở vị trí so le trong => AB//CD

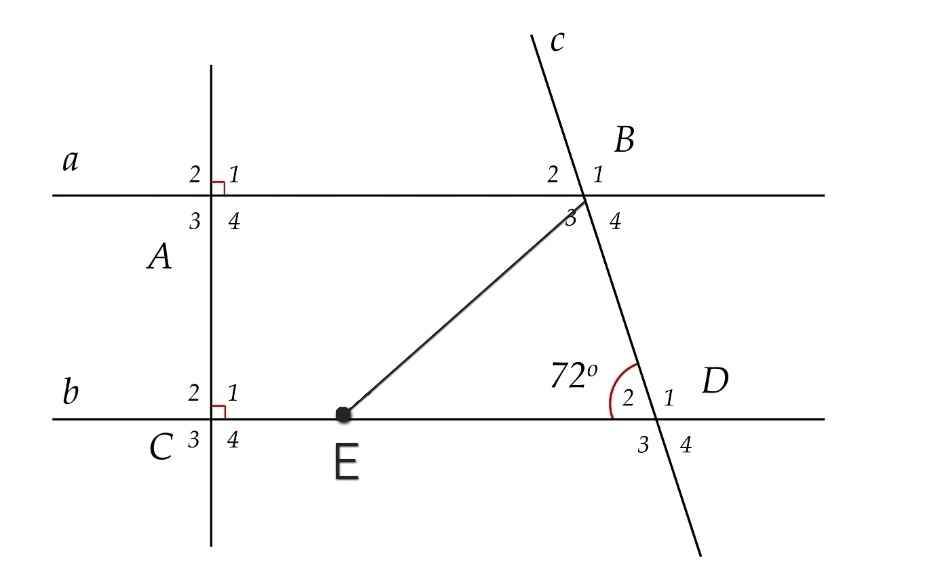 a) Ta có:
a) Ta có:
∠A₁ = ∠C₁ = 90⁰
Mà ∠A₁ và ∠C₁ là hai góc đồng vị
⇒ a // b
b) Ta có:
∠D₁ + ∠D₂ = 180⁰ (kề bù)
⇒ ∠D₁ = 180⁰ - ∠D₂
= 180⁰ - 72⁰
= 108⁰
Do a // b (cmt)
⇒ ∠ABD = ∠D₁ = 108⁰ (so le trong)
c) Do BE là tia phân giác của ∠ABD
⇒ ∠ABE = ∠ABD : 2
= 108⁰ : 2
= 54⁰

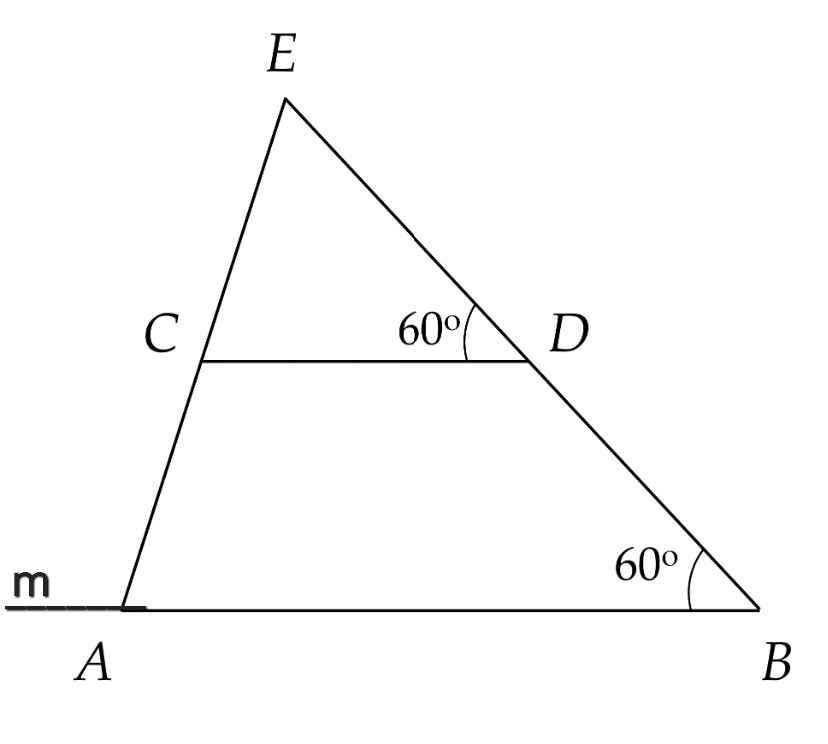
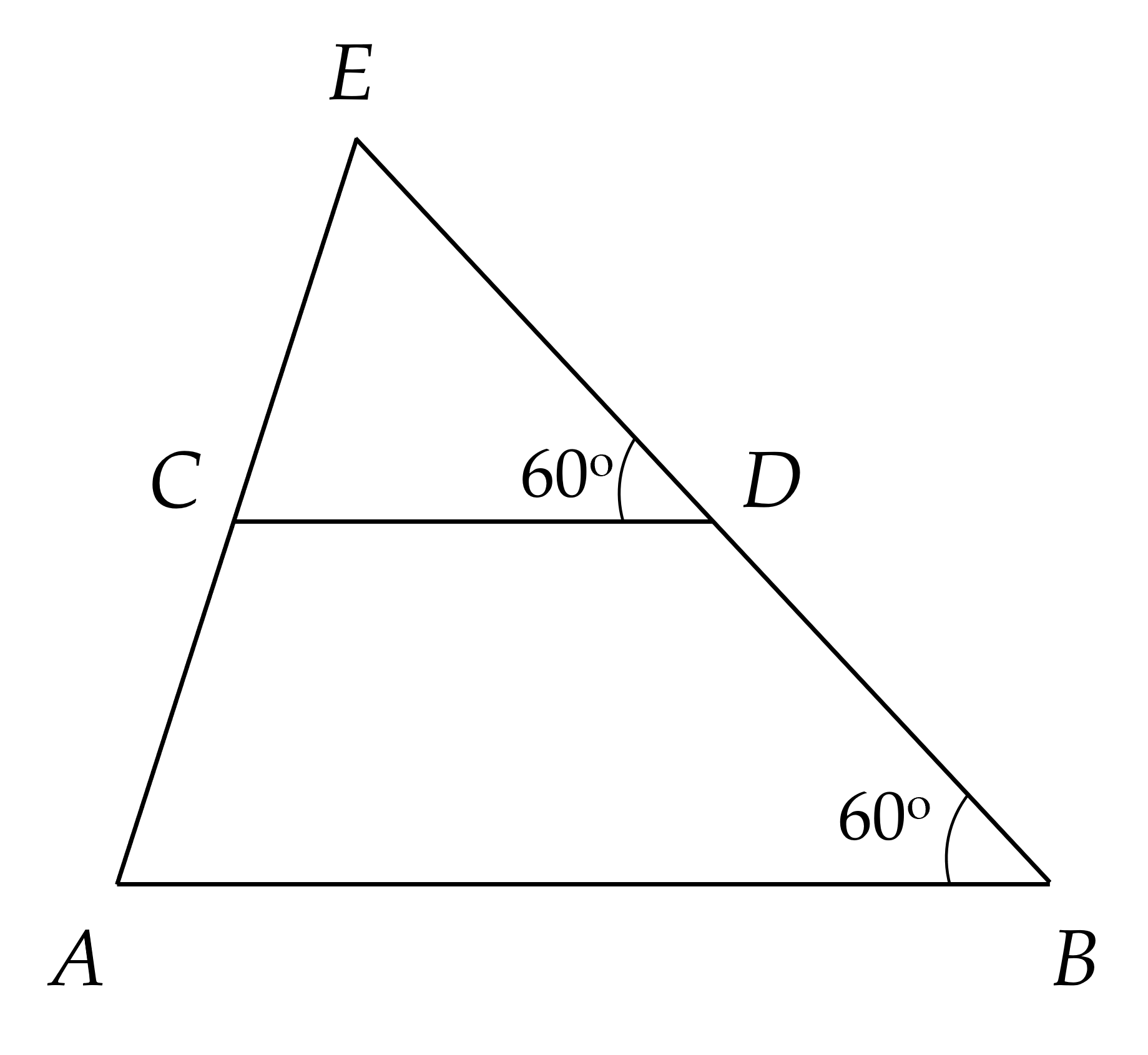
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

2 . seafood
3 . bulid sandcastle
4 . fireman
5 . brush the teeth
6 . basketball
7 . apple
1 . sit down
2 . seafood
3 . sand castle
4 . annoyed
5 . toothpaste
6 .basketball
7 . delicate
8 . honey

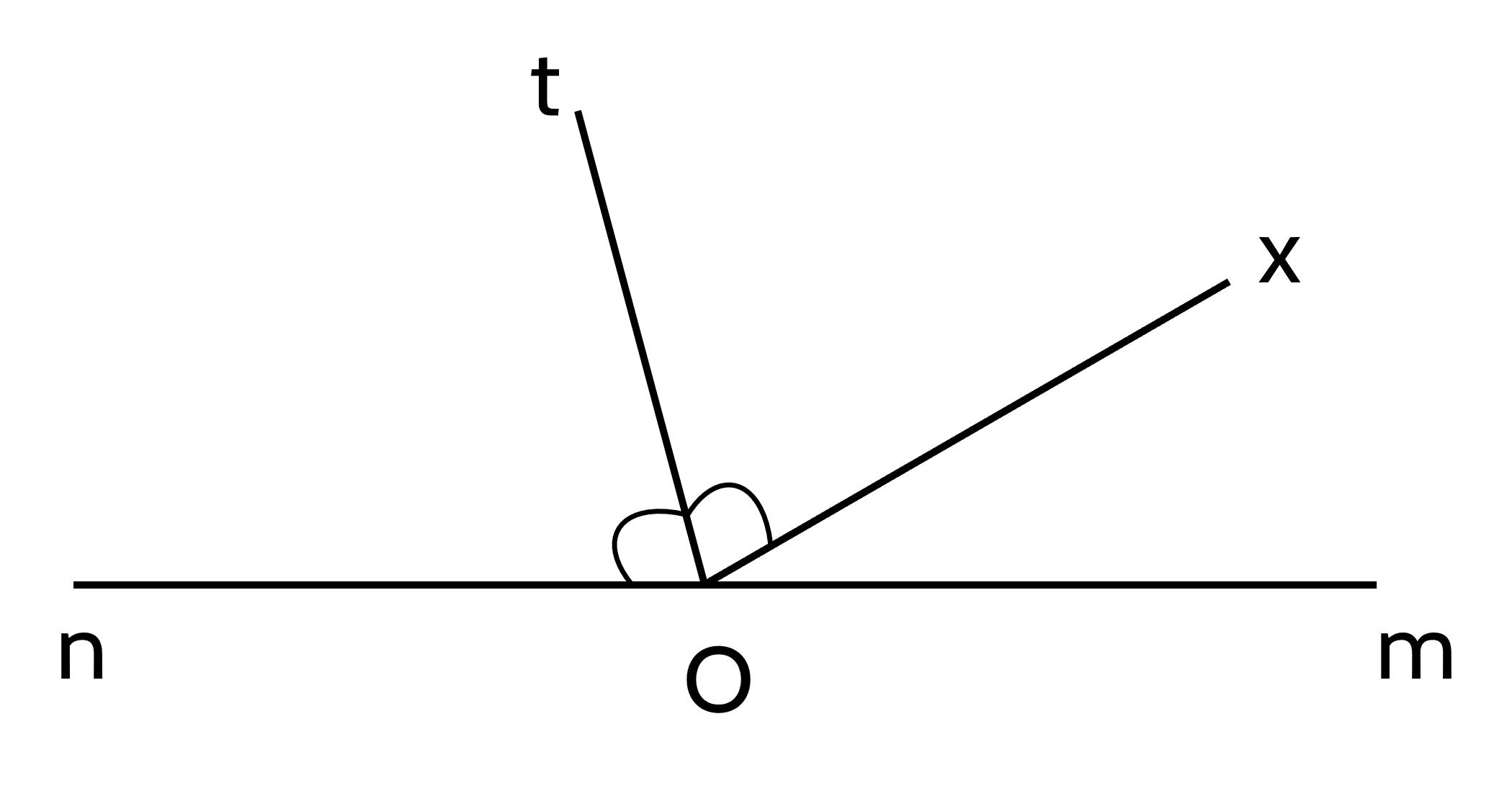
a) Ta có:
∠mOx + ∠nOx = 180⁰ (kề bù)
⇒ ∠nOx = 180⁰ - ∠mOx
= 180⁰ - 30⁰
= 150⁰
Do Ot là tia phân giác của ∠nOx
⇒ ∠nOt = ∠nOx : 2
= 150⁰ : 2
= 75⁰
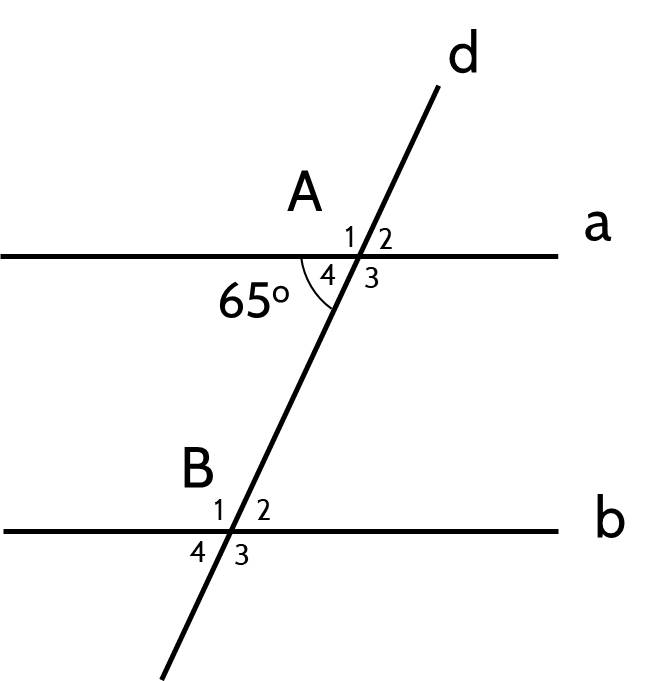
b) Do a // b
⇒ ∠B₄ = ∠A₄ = 65⁰ (đồng vị)
Ta có:
∠B₃ + ∠B₄ = 180⁰ (kề bù)
⇒ ∠B₃ = 180⁰ - ∠B₄
= 180⁰ - 65⁰
= 115⁰
Tính số đo góc �3^B3.
Hướng dẫn giải:a) ���^+���^=180∘mOx+xOn=180∘
Vậy ���^=180∘−30∘=150∘nOx=180∘−30∘=150∘.
��Ot là tia phân giác của ���^nOx, suy ra ���^=12.���^=75∘nOt=21.nOx=75∘.
b) a // b suy ra �4^=�2^=65∘A4=B2=65∘ (hai góc so le trong).
Mặt khác, ta có �2^+�3^=180∘B2+B3=180∘
Suy ra �3^=180∘−�2^=115∘B3=180∘−B2=115∘.


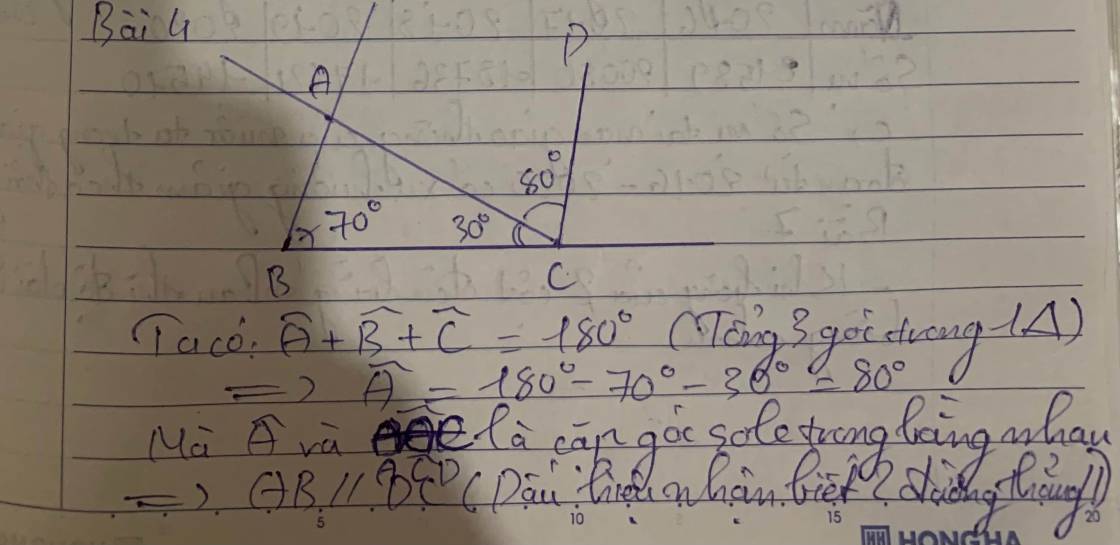









|\(x^2-25\)| + |y - 1| = 0
Vì |\(x^2\) - 25| ≥ 0; | y -1| ≥ 0 ∀ \(x\) ; y
Nên |\(x^2-25\)| + |y - 1| = 0 khi và chỉ khi:
\(\begin{cases}x^2-25=0\\ y-1=0\end{cases}\)
\(\begin{cases}\left[\begin{array}{l}x=-5\\ x=5\end{array}\right.\\ y=1\end{cases}\)
Vậy (\(x;y\) ) = (-5; 1); (5; 1)