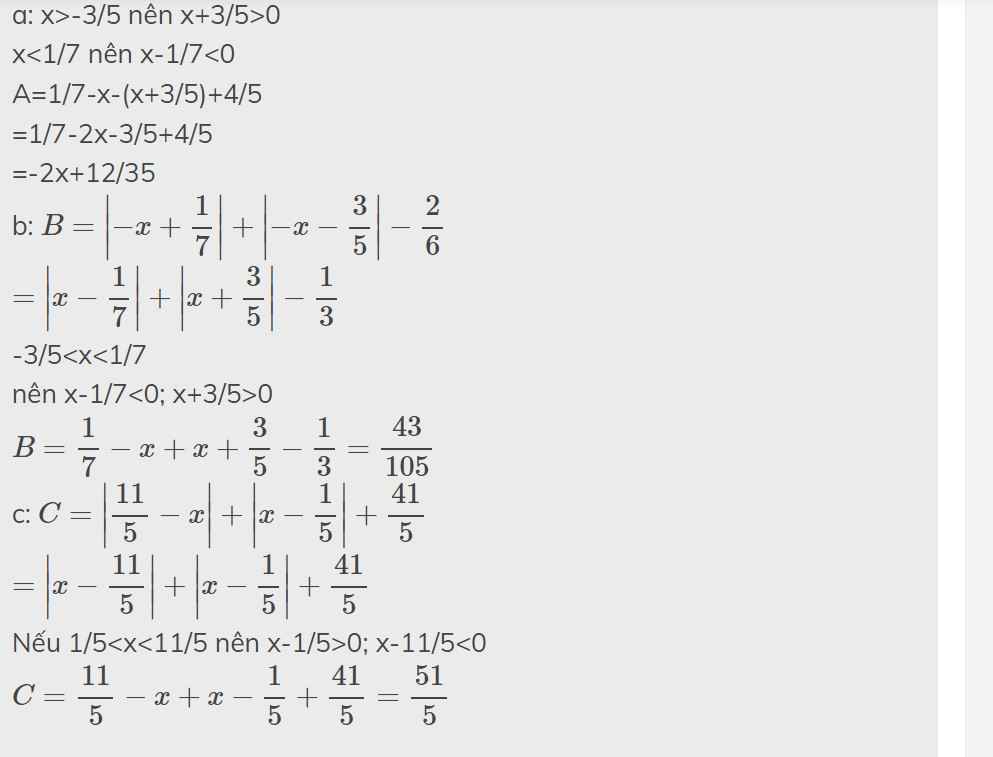Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: x>-3/5 nên x+3/5>0
x<1/7 nên x-1/7<0
A=1/7-x-(x+3/5)+4/5
=1/7-2x-3/5+4/5
=-2x+12/35
b: \(B=\left|-x+\dfrac{1}{7}\right|+\left|-x-\dfrac{3}{5}\right|-\dfrac{2}{6}\)
\(=\left|x-\dfrac{1}{7}\right|+\left|x+\dfrac{3}{5}\right|-\dfrac{1}{3}\)
-3/5<x<1/7
nên x-1/7<0; x+3/5>0
\(B=\dfrac{1}{7}-x+x+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{43}{105}\)
c: \(C=\left|\dfrac{11}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
\(=\left|x-\dfrac{11}{5}\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
Nếu 1/5<x<11/5 nên x-1/5>0; x-11/5<0
\(C=\dfrac{11}{5}-x+x-\dfrac{1}{5}+\dfrac{41}{5}=\dfrac{51}{5}\)

a: x>-3/5 nên x+3/5>0
x<1/7 nên x-1/7<0
A=1/7-x-(x+3/5)+4/5
=1/7-2x-3/5+4/5
=-2x+12/35
b: \(B=\left|-x+\dfrac{1}{7}\right|+\left|-x-\dfrac{3}{5}\right|-\dfrac{2}{6}\)
\(=\left|x-\dfrac{1}{7}\right|+\left|x+\dfrac{3}{5}\right|-\dfrac{1}{3}\)
-3/5<x<1/7
nên x-1/7<0; x+3/5>0
\(B=\dfrac{1}{7}-x+x+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{43}{105}\)
c: \(C=\left|\dfrac{11}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
\(=\left|x-\dfrac{11}{5}\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
Nếu 1/5<x<11/5 nên x-1/5>0; x-11/5<0
\(C=\dfrac{11}{5}-x+x-\dfrac{1}{5}+\dfrac{41}{5}=\dfrac{51}{5}\)


a vì 3<x<5 suy ra x=4
suy ra |4-3|+|4-5|=1+12
b thay x=vì x>\(\frac{-1}{2}\) suy ra 2x+1 >hoặc bằng 0
suy ra |2x+1|-|2x+1|=0

ta có
\(\left|x+1\right|+\left|x\right|=3\)
vì \(\left|x+1\right|\ge0\)và \(\left|x\right|\ge0\)
nên \(\left|x\right|+\left|x+1\right|=0+3=1+2=2+1=3+0\)
\(\Rightarrow\left|x\right|\in\left\{0;1;2;3\right\}\)
\(\Rightarrow x\in\left\{0;\pm1;\pm2;\pm3\right\}\)
mà \(x< -1\) nên \(x\in\left\{-2;-3\right\}\)

x<-1=>|x+1|=-x-1 và |x|=-x
=>-x-1-x=3
=>-2x=4=>x=-2