K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 5 2022
a: x>-3/5 nên x+3/5>0
x<1/7 nên x-1/7<0
A=1/7-x-(x+3/5)+4/5
=1/7-2x-3/5+4/5
=-2x+12/35
b: \(B=\left|-x+\dfrac{1}{7}\right|+\left|-x-\dfrac{3}{5}\right|-\dfrac{2}{6}\)
\(=\left|x-\dfrac{1}{7}\right|+\left|x+\dfrac{3}{5}\right|-\dfrac{1}{3}\)
-3/5<x<1/7
nên x-1/7<0; x+3/5>0
\(B=\dfrac{1}{7}-x+x+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{43}{105}\)
c: \(C=\left|\dfrac{11}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
\(=\left|x-\dfrac{11}{5}\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
Nếu 1/5<x<11/5 nên x-1/5>0; x-11/5<0
\(C=\dfrac{11}{5}-x+x-\dfrac{1}{5}+\dfrac{41}{5}=\dfrac{51}{5}\)
21 tháng 5 2022
a: x>-3/5 nên x+3/5>0
x<1/7 nên x-1/7<0
A=1/7-x-(x+3/5)+4/5
=1/7-2x-3/5+4/5
=-2x+12/35
b: \(B=\left|-x+\dfrac{1}{7}\right|+\left|-x-\dfrac{3}{5}\right|-\dfrac{2}{6}\)
\(=\left|x-\dfrac{1}{7}\right|+\left|x+\dfrac{3}{5}\right|-\dfrac{1}{3}\)
-3/5<x<1/7
nên x-1/7<0; x+3/5>0
\(B=\dfrac{1}{7}-x+x+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{43}{105}\)
c: \(C=\left|\dfrac{11}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
\(=\left|x-\dfrac{11}{5}\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
Nếu 1/5<x<11/5 nên x-1/5>0; x-11/5<0
\(C=\dfrac{11}{5}-x+x-\dfrac{1}{5}+\dfrac{41}{5}=\dfrac{51}{5}\)
18 tháng 9 2016
1/ \(\frac{1}{3x}:\frac{2}{3}=1\)
<=> \(\frac{3}{3×2×x}=\:1\)
<=> \(\frac{1}{2x}=1\)<=> x = \(\frac{1}{2}\)
19 tháng 7 2021
a, \(\left(3x-5\right)\left(x+1\right)-\left(3x-1\right)\left(x+1\right)=x-4\)
\(\Leftrightarrow\left(x+1\right)\left(3x-5-3x+1\right)=x-4\Leftrightarrow-4\left(x+1\right)=x-4\)
\(\Leftrightarrow-4x-4=x-4\Leftrightarrow-4x-x=0\Leftrightarrow x=0\)
b, \(\left(x-2\right)\left(x+3\right)-\left(x+4\right)\left(x-7\right)=5-x\)
\(\Leftrightarrow x^2+x-6-x^2-3x+28=5-x\Leftrightarrow-2x+22=5-x\Leftrightarrow x=17\)
c, thiếu đề
d, \(3\left(x-7\right)\left(x+7\right)-\left(x-1\right)\left(3x+2\right)=13\)
\(\Leftrightarrow3x^2-147-3x^2+x+2=13\Leftrightarrow x=11+147=158\)
NM
Nguyễn Minh Quang
Giáo viên
19 tháng 7 2021
a.\(3x^2-2x-5-\left(3x^2+2x-1\right)=x-4\)
\(\Leftrightarrow-5x=0\Leftrightarrow x=0\)
b.\(x^2+x-6-\left(x^2-3x-28\right)=5-x\)
\(\Leftrightarrow5x=-17\Leftrightarrow x=-\frac{17}{5}\)
c.\(5\left(x^2-10x+21\right)-\left(5x^2-9x-2\right)=0\)
\(\Leftrightarrow-41x+107=0\Leftrightarrow x=\frac{107}{41}\)
d.\(3\left(x^2-49\right)-\left(3x^2-x-2\right)=13\Leftrightarrow x=158\)
23 tháng 5 2022
Bài 1:
1: 7/20-|x+2/5|=10/21
=>|x+2/5|=-53/420(vô lý)
2: \(\left|\dfrac{3}{7}-x\right|-\left(-\dfrac{2}{3}\right)=1+\dfrac{1}{2}\)
\(\Leftrightarrow\left|x-\dfrac{3}{7}\right|=\dfrac{3}{2}-\dfrac{2}{3}=\dfrac{5}{6}\)
=>x-3/7=5/6 hoặc x-3/7=-5/6
=>x=53/42 hoặc x=-17/42
TV
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 9
Bài 1:
a; \(\dfrac{7}{8}\) + \(x\) = \(\dfrac{4}{7}\)
\(x\) = \(\dfrac{4}{7}\) - \(\dfrac{7}{8}\)
\(x\) = \(\dfrac{32}{56}\) - \(\dfrac{49}{56}\)
\(x=-\) \(\dfrac{49}{56}\)
Vậy \(x=-\dfrac{49}{56}\)
b; 6 - \(x\) = - \(\dfrac{3}{4}\)
\(x\) = 6 + \(\dfrac{3}{4}\)
\(x\) = \(\dfrac{24}{4}+\dfrac{3}{4}\)
\(x=\dfrac{27}{4}\)
Vậy \(x=\dfrac{27}{4}\)
c; \(\dfrac{1}{-5}\) + \(x\) = \(\dfrac{3}{4}\)
\(x\) = \(\dfrac{3}{4}\) + \(\dfrac{1}{5}\)
\(x=\dfrac{15}{20}\) + \(\dfrac{4}{20}\)
\(x=\dfrac{19}{20}\)
Vậy \(x=\dfrac{19}{20}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 9
Bài 1:
d; - 6 - \(x\) = - \(\dfrac{3}{5}\)
\(x\) = - 6 + \(\dfrac{3}{5}\)
\(x=-\dfrac{30}{5}\) + \(\dfrac{3}{5}\)
\(x=-\dfrac{27}{5}\)
Vậy \(x=-\dfrac{27}{5}\)
e; - \(\dfrac{2}{6}\) + \(x\) = \(\dfrac{5}{7}\)
\(x\) = \(\dfrac{5}{7}\) + \(\dfrac{2}{6}\)
\(x\) = \(\dfrac{15}{21}\) + \(\dfrac{1}{3}\)
\(x=\dfrac{15}{21}\) + \(\dfrac{7}{21}\)
\(x=\dfrac{22}{21}\)
Vậy \(x=\dfrac{22}{21}\)
f; - 8 - \(x\) = - \(\dfrac{5}{3}\)
\(x\) = \(-\dfrac{5}{3}\) + 8
\(x\) = \(\dfrac{-5}{3}\) + \(\dfrac{24}{3}\)
\(x\) = \(\dfrac{-19}{3}\)
Vậy \(x=-\dfrac{19}{3}\)
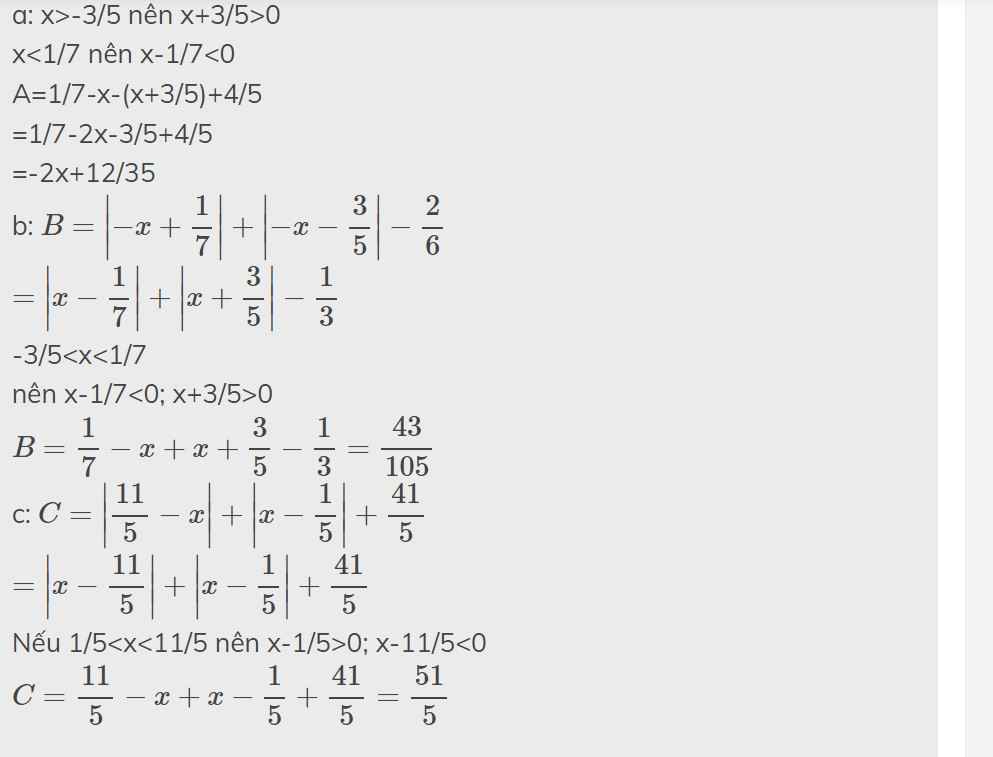
(x+1)7=(x+1)5
=>(x+1)7-(x+1)5=0
=>(x+1)2x(x+1)5-(x+1)5=0
=>(x+1)5x(x+12-1)=0
=>x=0;-1-2
(\(x+1\))7 = (\(x\) + 1)5
(\(x\) + 1)7 - (\(x\) + 1)5 = 0
(\(x\) + 1)5{(\(x\) + 1)2 - 1) = 0
\(\left[{}\begin{matrix}\left(x+1\right)^5=0\\\left(x+1\right)^2-1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x+1=0\\\left(x+1\right)^2=1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x+1=1\\x+1=-1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=0\\x=-2\end{matrix}\right.\)
Vậy \(x\) \(\in\){ -2; -1; 0}