
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{5x+7}{4}+\frac{3x+5}{8}>\frac{9x+4}{5}\)
\(\frac{10\cdot\left(5x+7\right)}{40}+\frac{5\cdot\left(3x+5\right)}{40}>\frac{8\cdot\left(9x+4\right)}{40}\)
10.(5x + 7) + 5.(3x + 5) > 8.(9x + 4)
10.(5x + 7) + 5.(3x + 5) - 8.(9x + 4) > 0
50x + 70 + 15x + 25 - 72x - 32 > 0
- 7x + 63 > 0
- 7.(x - 9) > 0
\(\Rightarrow x-9

`Answer:`
`x/y=5/7`
`=>k=x/5=y/7`
`=>x=5k;y=7k`
`=>C=\frac{5.5k-7k}{3.5k-2.7k}`
`=>C=\frac{25k-7k}{15k-14k}`
`=>C=\frac{k.(25-7)}{k.(15-14)}`
`=>C=18`


\(\left|x+6\right|-9=2x\)
\(\Rightarrow\left[\begin{array}{nghiempt}x+6-9=2x\\x-6+9=2x\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}x-2x=-6+9\\x-2x=6-9\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}-x=3\\-x=-3\end{array}\right.\)
Vậy \(x=-3\)

\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG
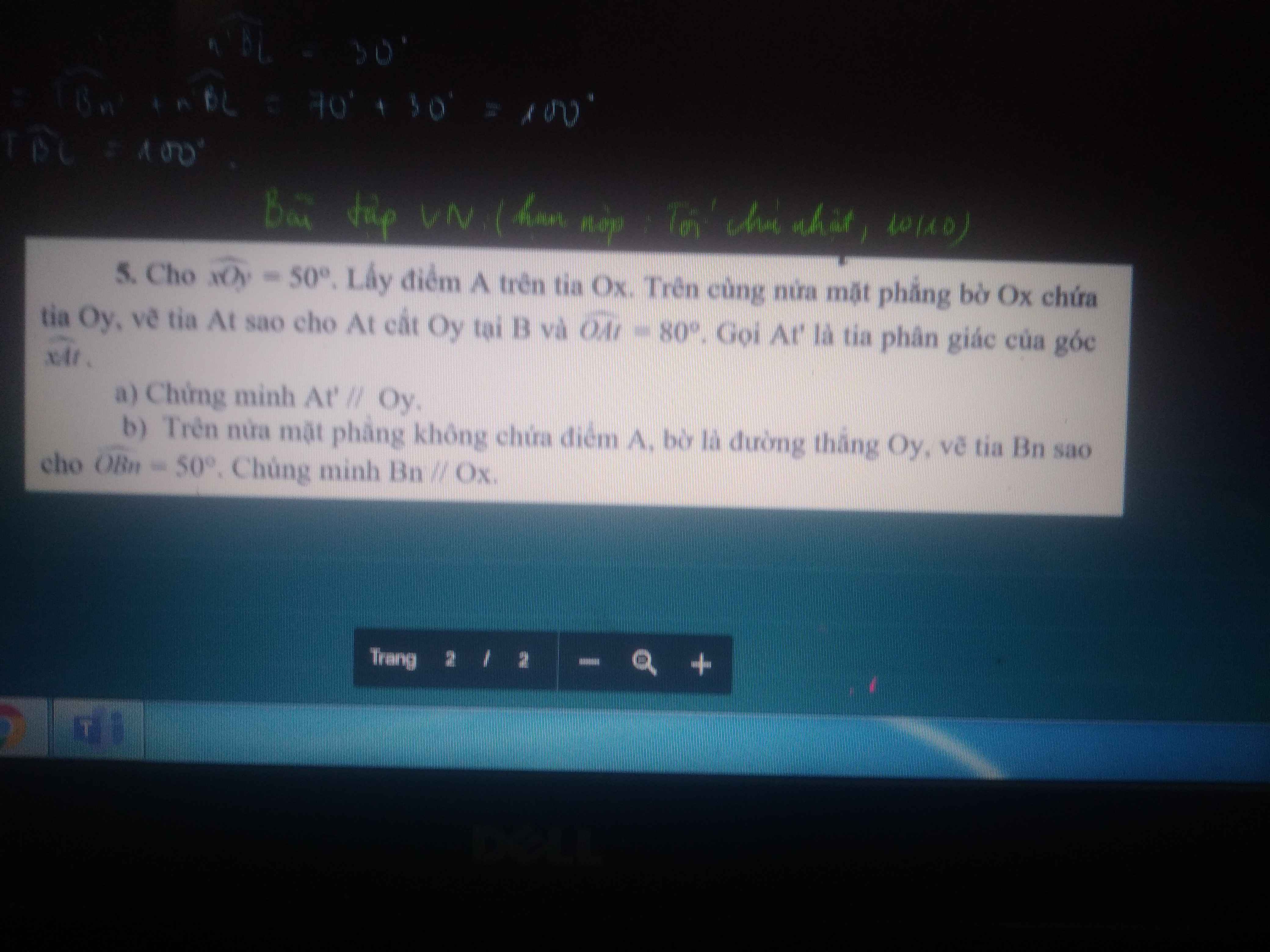
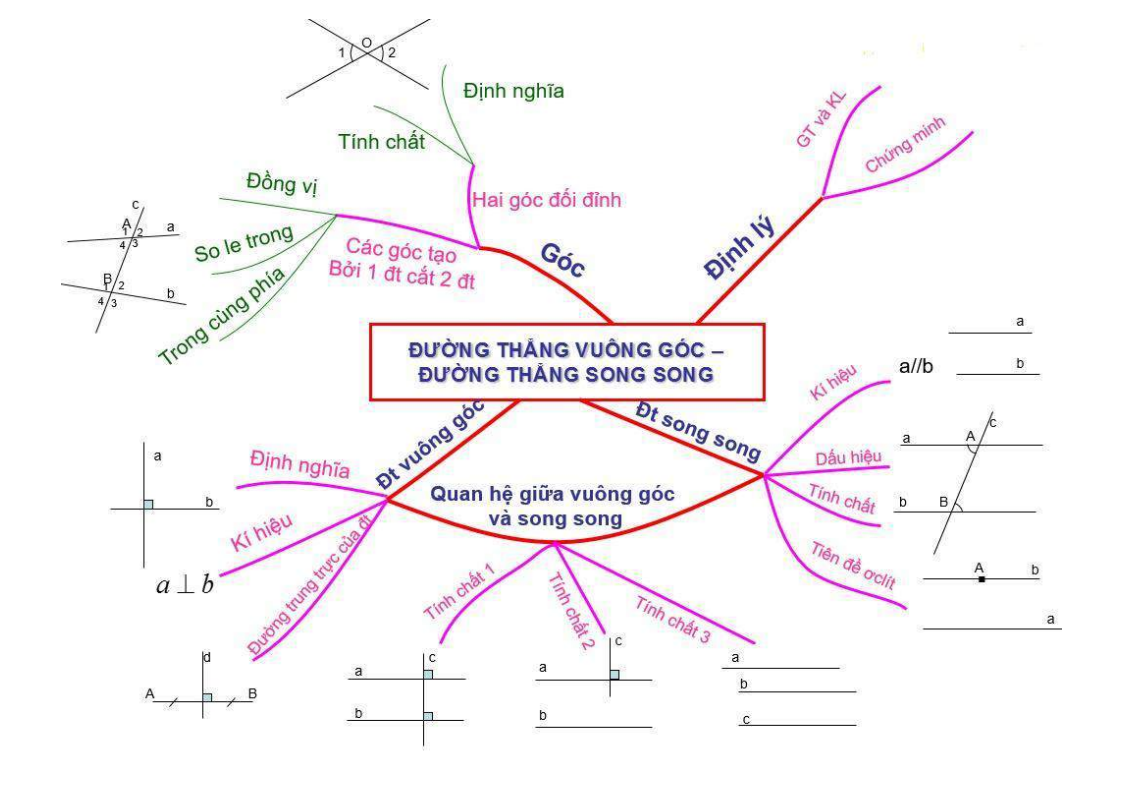
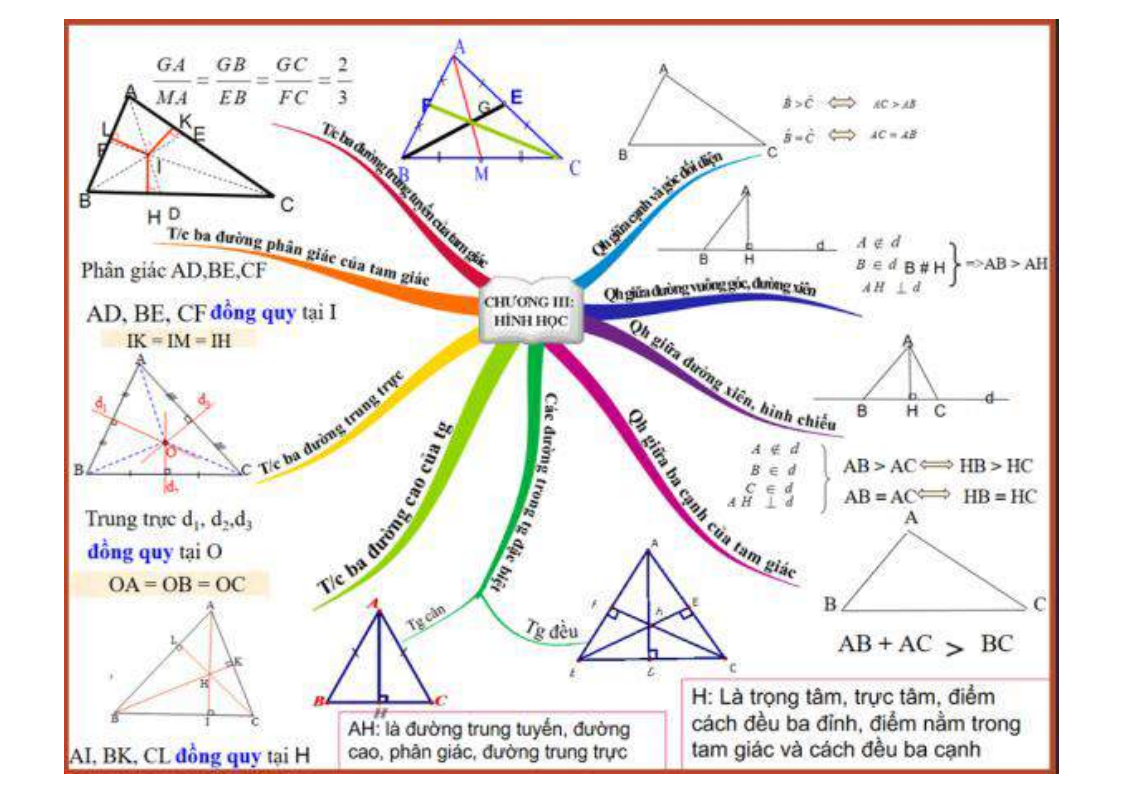
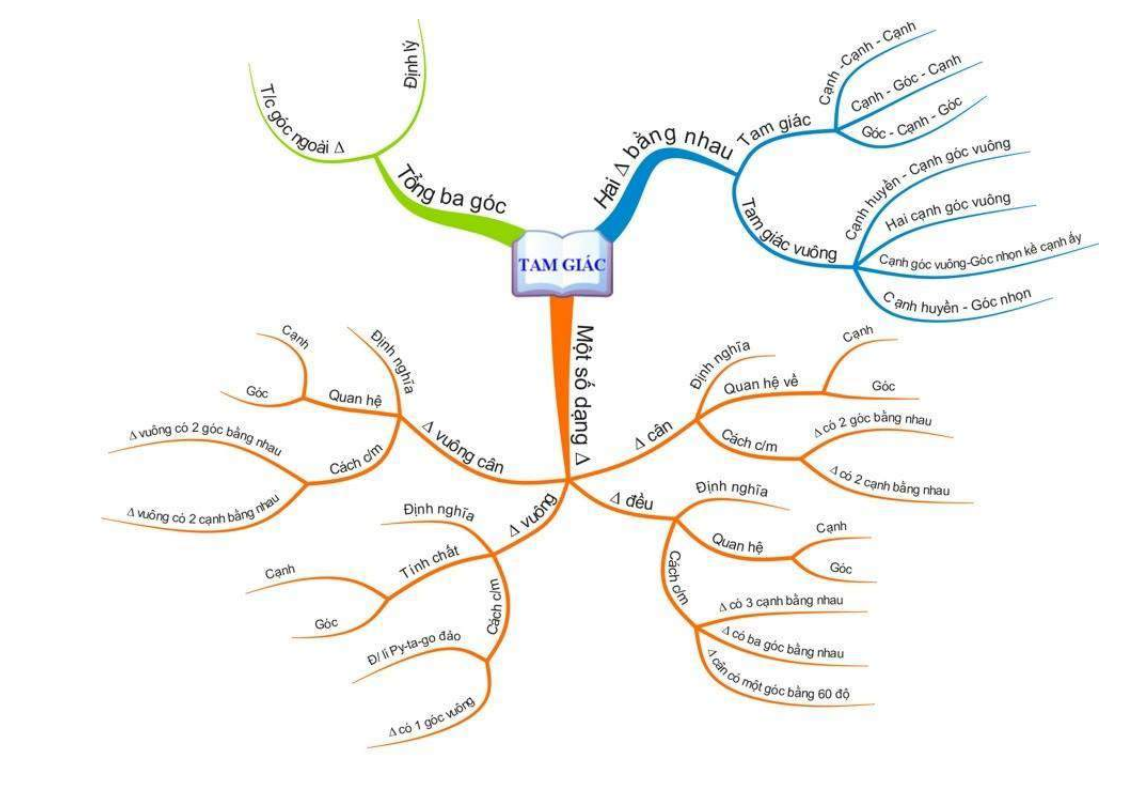
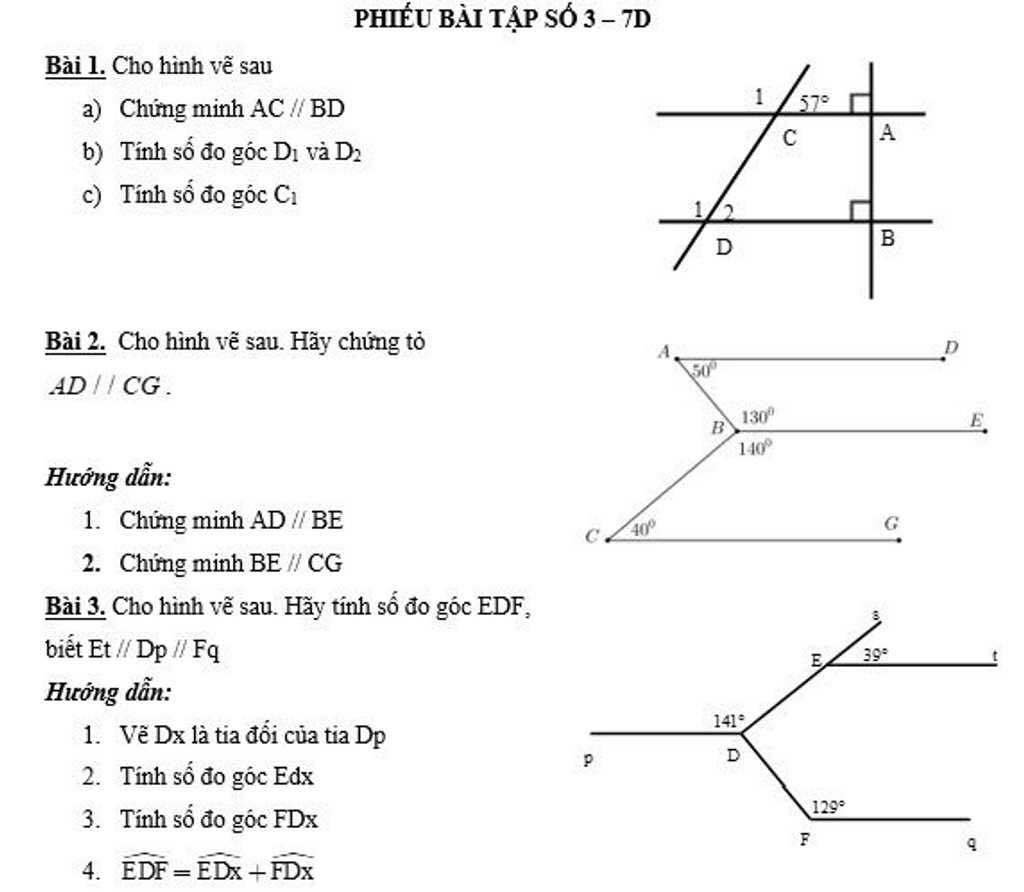 Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
\(\left|x-7\right|+\left|x-10\right|=3\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x-7=3\\x-10=3\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=10\\x=13\end{array}\right.\)
Vậy \(x\in\left\{10;13\right\}\)
Ta có
\(\left|x-7\right|+\left|x-10\right|=\left|x-7\right|+\left|10-x\right|\)
Vì \(\begin{cases}\left|x-7\right|\ge x-7\\\left|10-x\right|\ge10-x\end{cases}\)\(\Rightarrow\left|x-7\right|+\left|10-x\right|\ge\left(x-7\right)+\left(10-x\right)\)
\(\Rightarrow\left|x-7\right|+\left|10-x\right|\ge3\)
Dấu " = " xảy ra khi \(\begin{cases}x-7\ge0\\10-x\ge0\end{cases}\)\(\Rightarrow\left[\begin{array}{nghiempt}x\ge7\\x\le10\end{array}\right.\)
Vậy \(x\in\left\{7;8;9;10\right\}\)