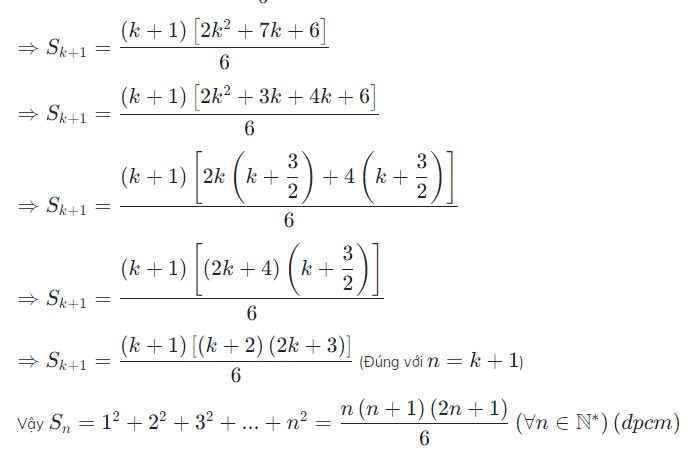Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mỗi số khi chia cho 3 thì xảy ra 1 trong 3 trường hợp sau:
n=3k;n=3k+1;n=3k+2 (k là số tự nhiên)
+ Nếu n= 3k thì=> n(n+2)(n+13) chia hết cho 3. (1)
+Nếu n=3k+1 => :n(n+2)(n+13)=(3k+1)(3k+1+2)(3k+1+13)
=(3k+1)(3k+3)(3k+14)
=(3k+1)(k+1)3(3k+14)
Vì 3 chia hết cho 3=>(3k+1)(k+1)3(3k+14) chia hết cho 3.
Hay n(n+2)(n+13) chia hết cho 3. (2)
+Nếu n=3k+2 =>n(n+2)(n+13)=(3k+2)(3k+2+2)(3k+2+13)
=(3k+2)(3k+4)(3k+15)
=(3k+2)(3k+4)(k+5)3
Vì 3 chia hết cho 3=>(3k+2)(3k+4)(k+5)3 chia hết cho 3.
Hay n(n+2)(n+13) chia hết cho 3. (3)
Từ (1),(2) và (3) => với mọi số tự nhiên n thì n(n+2)(n+13) chia hết cho 3.
Vậy với mọi số tự nhiên n thì n(n+2)(n+13) chia hết cho 3.

Bước 1: Chứng minh công thức đúng cho n = 1. Khi n = 1, ta có: 1² = 1 = 1 . (1 + 1) . (2 . 1 + 1) / 6 = 1. Vậy công thức đúng cho n = 1.
Bước 2: Giả sử công thức đúng cho n = k, tức là 1² + 2² + ... + k² = k . (k + 1) . (2k + 1) / 6. Ta cần chứng minh công thức đúng cho n = k + 1, tức là 1² + 2² + ... + k² + (k + 1)² = (k + 1) . (k + 1 + 1) . (2(k + 1) + 1) / 6.
Bước 3: Chứng minh công thức đúng cho n = k + 1. Ta có: 1² + 2² + ... + k² + (k + 1)² = (k . (k + 1) . (2k + 1) / 6) + (k + 1)² = (k . (k + 1) . (2k + 1) + 6(k + 1)²) / 6 = (k . (k + 1) . (2k + 1) + 6(k + 1) . (k + 1)) / 6 = (k + 1) . ((k . (2k + 1) + 6(k + 1)) / 6) = (k + 1) . ((2k² + k + 6k + 6) / 6) = (k + 1) . ((2k² + 7k + 6) / 6) = (k + 1) . ((k + 2) . (2k + 3) / 6) = (k + 1) . ((k + 1 + 1) . (2(k + 1) + 1) / 6).
Vậy, công thức đã được chứng minh đúng cho mọi số tự nhiên n khác 0.

Chắc chắn sai đề vì n(n+1) luôn là số lẻ làm sao mà chia hết cho 2 được

Bài giải
Theo đề bài, ta có: \(\frac{n^2+5n+15}{25}\)với n \(\in\)N
\(\frac{n^2+5n+15}{25}\)
= \(\frac{n^2}{25}+\frac{5n}{25}+\frac{15}{25}\)
Vì 15 không chia hết cho 25
Nên \(\frac{n^2+5n+15}{25}\notin Z\)
\(\RightarrowĐPCM\)