K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
30 tháng 9 2019

 Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.

a) Tìm nghiệm tổng quát của mỗi phương trình trên.

b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong cùng một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.
#Toán lớp 9
1
CM
Cao Minh Tâm
30 tháng 9 2019

a) + Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4

Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).

+ Xét phương trình 3x + 2y = 5 (2) ⇔ 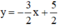Giải bài 7 trang 12 SGK Toán 9 Tập 2 | Giải toán lớp 9

Vậy phương trình (2) có nghiệm tổng quát là : 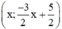Giải bài 7 trang 12 SGK Toán 9 Tập 2 | Giải toán lớp 9 (x ∈ R).

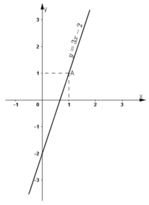
b) Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.

Chọn x = 0 ⇒ y = 4

Chọn y = 0 ⇒ x = 2.

⇒ (d) đi qua hai điểm (0; 4) và (2; 0).

Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) : 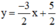Giải bài 7 trang 12 SGK Toán 9 Tập 2 | Giải toán lớp 9

Chọn x = 0 ⇒ y = 2,5.

Chọn y = 0 ⇒ 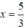Giải bài tập Toán lớp 9 | Giải Toán lớp 9

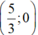
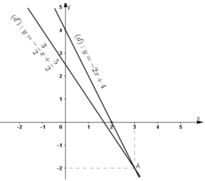
⇒ (d’) đi qua hai điểm (0; 2,5) và Giải bài 7 trang 12 SGK Toán 9 Tập 2 | Giải toán lớp 9

Giải bài 7 trang 12 SGK Toán 9 Tập 2 | Giải toán lớp 9

Hai đường thẳng cắt nhau tại A(3; -2).

Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2).

Đúng(1)
PT
Pham Trong Bach
25 tháng 12 2019

 Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.
#Toán lớp 9
1
CM
Cao Minh Tâm
25 tháng 12 2019

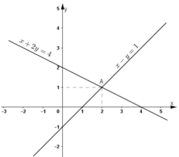
Giải bài 3 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9

- Vẽ đường thẳng x + 2y = 4.

   + Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).

   + Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).

Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).

- Vẽ đường thẳng x – y = 1

   + Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).

   + Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).

Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).

- Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).

- Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.

Đúng(0)
PT
Pham Trong Bach
21 tháng 6 2019

Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.
#Toán lớp 9
1
CM
Cao Minh Tâm
21 tháng 6 2019

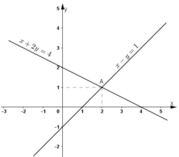
Giải bài 3 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9

- Vẽ đường thẳng x + 2y = 4.

   + Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).

   + Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).

Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).

- Vẽ đường thẳng x – y = 1

   + Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).

   + Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).

Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).

- Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).

- Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.

 

Đúng(0)
NL
Ngô Lê Xuân Thảo
11 tháng 2 2017 - olm

Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.

a) Tìm nghiệm tổng quát của mỗi phương trình trên.

b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong mỗi một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.
#Toán lớp 9
1
NL
Ngô Lê Xuân Thảo
11 tháng 2 2017

a) 2x+y=4⇔y=−2x+4⇔x=12−y+22x+y=4⇔y=−2x+4⇔x=12−y+2. Do đó phương trình có nghiệm dạng tổng quát như sau:

{x∈Ry=−2x+4{x∈Ry=−2x+4 hoặc {x=−12x+2y∈R{x=−12x+2y∈R

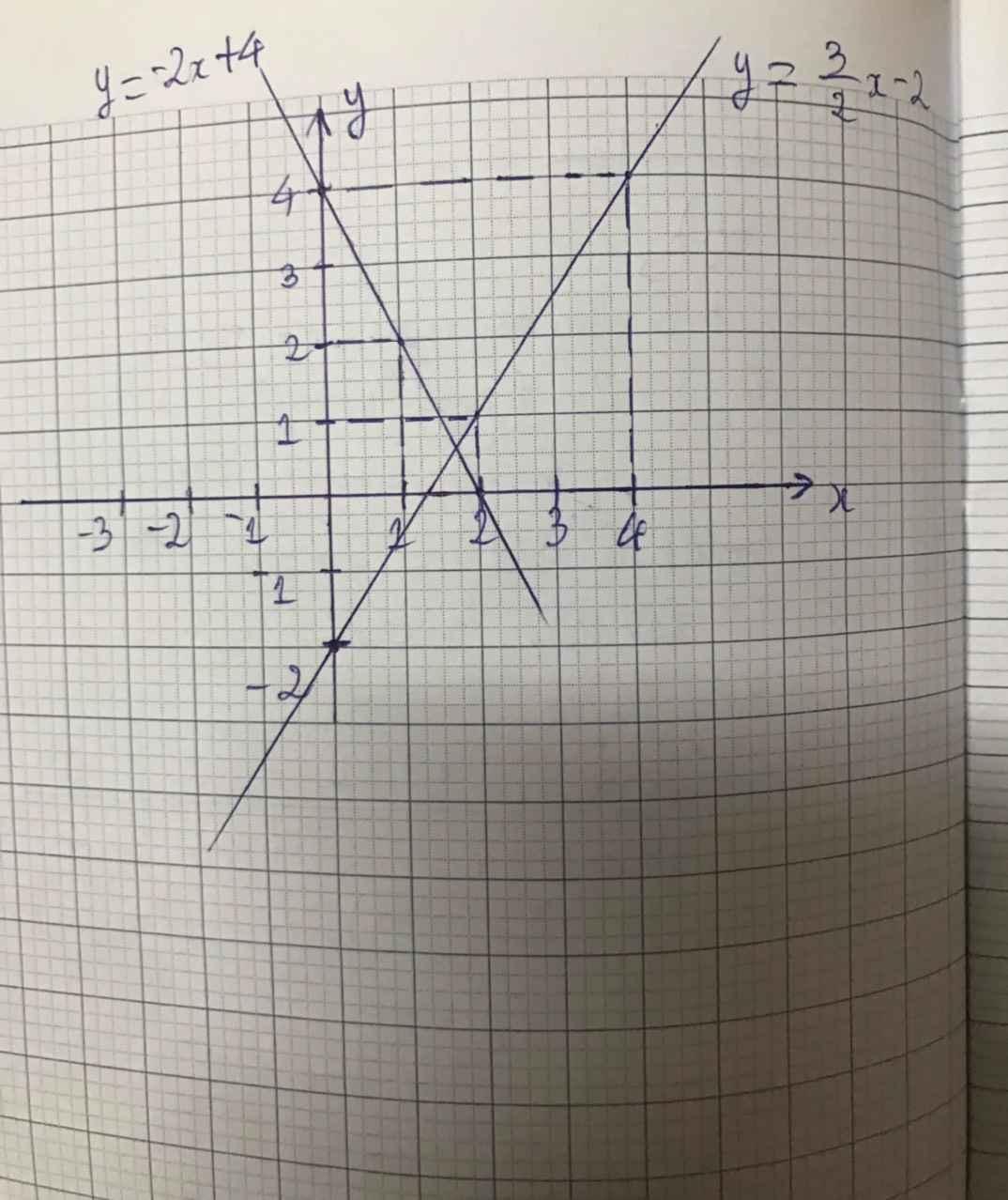
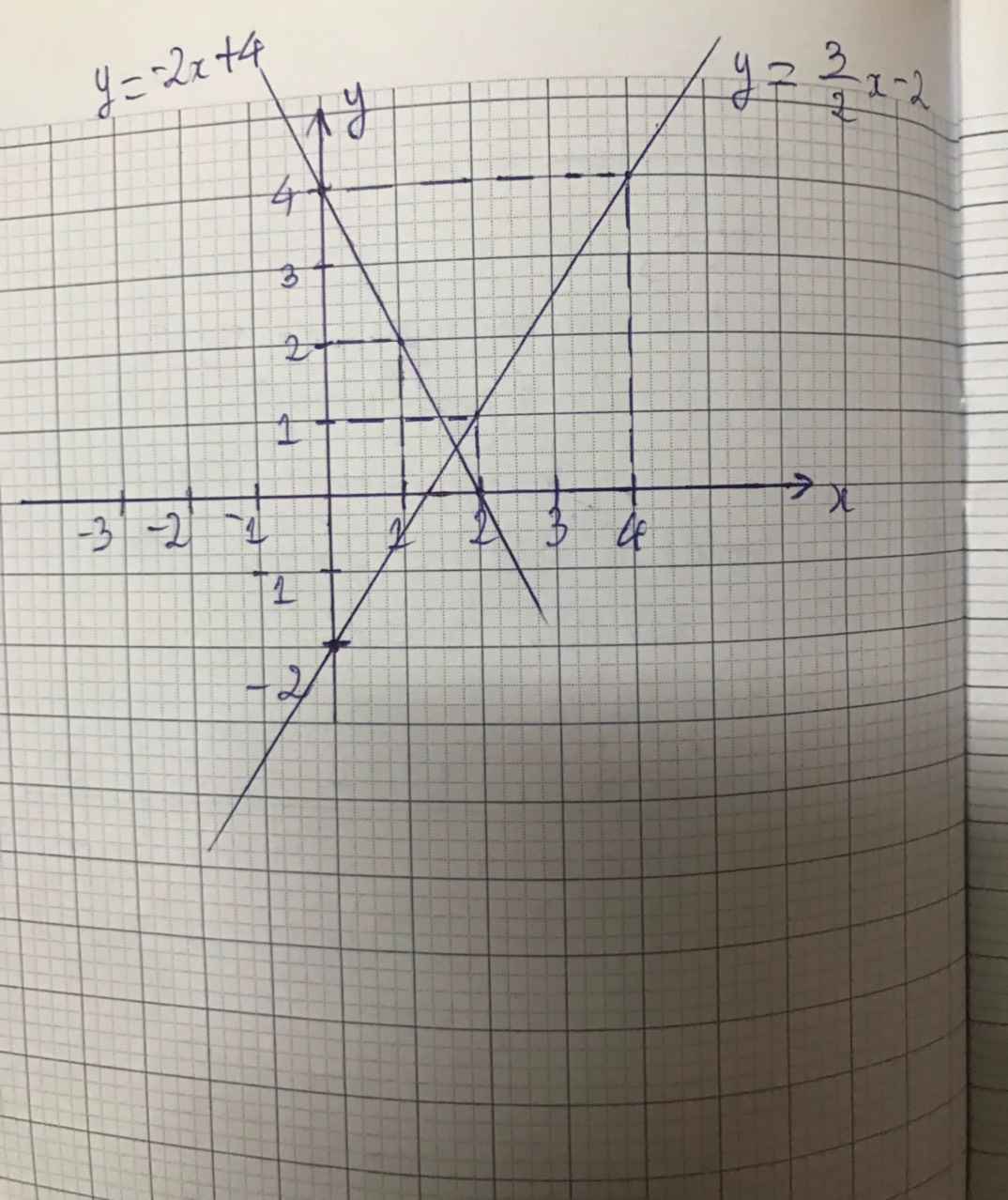
b) Vẽ (d1): 2x + y = 4

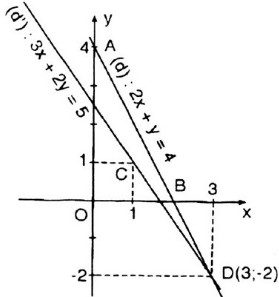
- Cho x = 0 => y = 4 được A(0; 4).

- Cho y = 0 => x = 2 được B(2; 0).

Vẽ (d2): 3x + 2y = 5

- Cho x = 0 => y =  được C(0; ).

- Cho y = 0 => x =  được D(; 0).

Hai đường thẳng cắt nhau tại M(3; -2).

Thay x = 3, y = -2 vào từng phương trình ta được:

2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)

Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.

Đúng(0)
PT
Pham Trong Bach
2 tháng 11 2017

Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.

Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong cùng một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.
#Toán lớp 9
1
CM
Cao Minh Tâm
2 tháng 11 2017

Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.

Chọn x = 0 ⇒ y = 4

Chọn y = 0 ⇒ x = 2.

⇒ (d) đi qua hai điểm (0; 4) và (2; 0).

Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) : 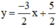Giải bài 7 trang 12 SGK Toán 9 Tập 2 | Giải toán lớp 9

Chọn x = 0 ⇒ y = 2,5.

Chọn y = 0 ⇒ 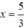Giải bài tập Toán lớp 9 | Giải Toán lớp 9

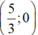
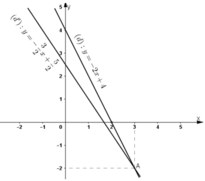
⇒ (d’) đi qua hai điểm (0; 2,5) và Giải bài 7 trang 12 SGK Toán 9 Tập 2 | Giải toán lớp 9

Giải bài 7 trang 12 SGK Toán 9 Tập 2 | Giải toán lớp 9

Hai đường thẳng cắt nhau tại A(3; -2).

Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2)

Đúng(0)
PT
Pham Trong Bach
14 tháng 8 2019

Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:

0x + 2y = 5
#Toán lớp 9
1
CM
Cao Minh Tâm
14 tháng 8 2019

0x + 2y = 5

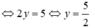
Giải bài tập Toán lớp 9 | Giải Toán lớp 9

Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).

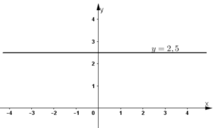
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.

Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng(0)
HT
Huỳnh Thảo Nguyên
6 tháng 4 2022

Cho Parabol y=x2 có đồ thị là (P).

a). Vẽ (P)

b). Gọi (D) là đường thẳng có phương trình y=-2x+b. Tìm b biết rằng (D) tiếp xúc với (P). Vẽ (D) và (P) trên cùng một hệ toạ độ. Xác định toạ độ giao điểm của chúng.
#Toán lớp 9
1
NL
Nguyễn Lê Phước Thịnh
6 tháng 4 2022

b: Phương trình hoành độ giao điểm là:

\(x^2+2x-b=0\)

Δ=4+4b

Để (P) tiếp xúc với (D) thì 4b+4=0

hay b=-1

Đúng(1)
PT
Pham Trong Bach
19 tháng 2 2019

Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó: x + 5y = 3
#Toán lớp 9
1
CM
Cao Minh Tâm
19 tháng 2 2019

x + 5y = 3 (2)

⇔ x = 3 – 5y

Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).

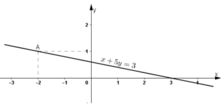
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.

   + Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).

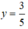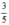   + Tại x = 0 thì Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9 ⇒ Đường thẳng đi qua điểm (0; Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9).

Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 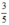Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9).

Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng(0)
PT
Pham Trong Bach
16 tháng 8 2017

Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó: 3x – y = 2
#Toán lớp 9
1
CM
Cao Minh Tâm
16 tháng 8 2017

3x – y = 2 (1)

⇔ y = 3x – 2.

Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).

Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).

   + Tại x = 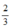Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (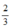Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9 ; 0).

   + Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).

Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (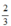Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9 ; 0) và (0; -2).

Giải bài 2 trang 7 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP