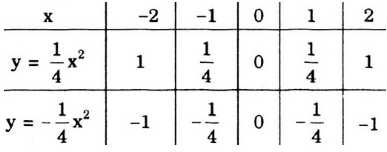
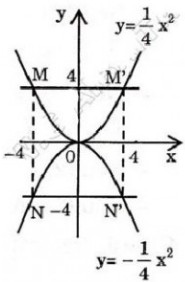
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4.
(1) => y=2m-mx thay vào (2) ta được x+m(2m-mx)=m+1
<=> x-m2x=-2m2+m+1
<=> x(1-m)(1+m)=-(m-1)(1+2m)
với m=-1 thì pt vô nghiệm
với m=1 thì pt vô số nghiệm => có nghiệm nguyên => chọn
với m\(\ne\pm\) 1 thì x=\(\frac{-2m-1}{m+1}\)=\(-2+\frac{1}{m+1}\)
=> y=2m-mx=xm-m(-2+\(\frac{1}{m+1}\)) =2m+2m-\(\frac{m}{m+1}\)=4m-1+\(\frac{1}{m+1}\)
để x y nguyên thì \(\frac{1}{m+1}\)nguyên ( do m nguyên)
=> m+1\(\in\)Ư(1)={1;-1}
=> m\(\in\){0;-2} mà m nguyên âm nên m=-2
vậy m=-2 thì ...
P/s hình như 1 2 3 sai đề

Mình gợi ý: Nếu pt có nghiệm \(x=t\) thì cũng có nghiệm \(x=-t\).
Vậy nếu pt có 4 nghiệm và giả sử \(a< b< c< d\) thì \(d=-a,c=-b\).
Vậy AB=CD là hiển nhiên.
Mình chỉ cần BC=CD. Tức là \(2c=d-c\Rightarrow d=3c\).
Đặt \(X=x^2\). Ta tìm m để pt mới (bậc 2) có 2 nghiệm dương thoả nghiệm này gấp 3 nghiệm kia.

a)Thay m=2 vào phương trình trên ta được:
\(3x^2+4\left(2-1\right)x-2^2=0\)
\(\Leftrightarrow3x^2+4x-4=0\)
\(\Leftrightarrow\left(x-\frac{2}{3}\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=-2\end{cases}}\)