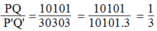Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(\frac{AB}{CD}=\frac{120}{480}=\frac{1}{4}\)
b, 10,5 dm = 105 cm
\(\frac{EF}{E'F'}=\frac{45}{105}=\frac{3}{7}\)
c, \(\frac{MN}{M'N'}=\frac{555}{999}=\frac{5}{9}\)
d, 303,03m = 30303cm
\(\frac{PQ}{P'Q'}=\frac{10101}{30303}=\frac{1}{3}\)
Chúc bạn học tốt!!

\(\frac{MN}{PQ}=\frac{3}{5}\Rightarrow\frac{MN}{3}=\frac{PQ}{5}=\frac{MN-PQ}{3-5}=\frac{12}{-2}\)
sai đề

đây là toán đại mà,tỉ lệ thức đo,từ đề ta suy ra tỉ lệ thức MN/3=PQ/5
sau đó tính như toán lớp 7 đó

a: Xét ΔMNP và ΔKPN có
\(\hat{MNP}=\hat{KPN}\) (hai góc so le trong, MN//PK)
PN chung
\(\hat{MPN}=\hat{KNP}\) (hai góc so le trong, MP//NK)
Do đó: ΔMNP=ΔKPN
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: ΔNQK cân tại N
=>\(\hat{NQK}=\hat{NKQ}\)
mà \(\hat{NKQ}=\hat{MPQ}\) (hai góc đồng vị, MP//NK)
nên \(\hat{MPQ}=\hat{NQP}\)
Xét ΔMPQ và ΔNQP có
MP=NQ
\(\hat{MPQ}=\hat{NQP}\)
QP chung
Do đó: ΔMPQ=ΔNQP
c: ΔMPQ=ΔNQP
=>\(\hat{MQP}=\hat{NPQ}\)
=>MNPQ là hình thang cân


Đổi: P'Q' : 303,03m = 30303 cm
Ta có: