K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

16 tháng 4 2017
a.\(\dfrac{3}{11}\)
b.\(\dfrac{-4}{7}\)
c.\(\dfrac{-5}{13}\)
d.\(\dfrac{x}{3}\)

18 tháng 5 2017
a) a=15a′(a′∈N)a=15a′(a′∈N)
b=15b′(b′∈N)b=15b′(b′∈N)
15 là ước chung của a và b.
b) a=15a′(a′∈N)a=15a′(a′∈N)
b=15b′(b′∈N)b=15b′(b′∈N)
ƯCLN(a′,b′)=1(a′,b′)=1
15 là ƯCLN của a và b.

16 tháng 4 2017
Không, vì số \(0\) cũng là một số nguyên nhưng không thuộc bộ phận các số dương cũng không thuộc bộ phận các số âm.
16 tháng 4 2017
Ko. Vì tập hợp số nguyên bao gồm số nguyên dương , số nguyên âm và số 0 . Mà đề cho có số nguyên âm và số nguyên dương thôi nên thiếu số 0 .
=> Câu này sai .
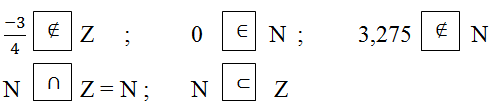
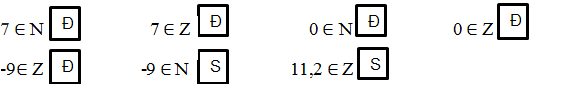
\(\text{Z}=\left\{...;-2;-1;0;1;2;....\right\}\)
\(Z=\left\{....;-200;-199;-198;...;-3;-2;-1;0;1;2;3;......\right\}\)