Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: 
Mà a = b + c nên 
Từ (1), (2) suy ra:
với a = b + c và a, b, c ∈ Z, b ≠ 0, c ≠ 0
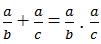
So sánh: \(\dfrac{434}{561}\) và \(\dfrac{441}{568}\)
* Bài làm:
Vì \(\dfrac{434}{561}\) < 1 => \(\dfrac{434}{561}\) < \(\dfrac{434+7}{561+7}\) hay \(\dfrac{434}{561}\) < \(\dfrac{441}{568}\)
a) \(\dfrac{a}{b}\)=\(\dfrac{a\left(b+m\right)}{b\left(b+m\right)}\)=\(\dfrac{ab+am}{b^2+bm}\) ; (1)
\(\dfrac{a+m}{b+m}\)=\(\dfrac{b\left(a+m\right)}{b\left(b+m\right)}\)=\(\dfrac{ab+bm}{b^2+bm}\) ; (2)
\(\dfrac{a}{b}\) < \(1\) \(\Rightarrow\) \(a\) < \(b\), suy ra \(ab+am\) < \(ab+bm\). (3)
Từ (1), (2) và (3) ta có: \(\dfrac{a}{b}\) < \(\dfrac{a+m}{b+m}\)
b) Áp dụng, rõ ràng \(\dfrac{434}{561}\) < 1 nên \(\dfrac{434}{561}\) < \(\dfrac{434+7}{561+7}\)=\(\dfrac{441}{568}\)
Không. Vì không có phân số nào mà cả tử số và mẫu số nhân với hai số khác nhau lại bằng phân số đã cho cả (hay do m khác n)
5.Phân số tối giản là phân số không thể rút gọn được nữa. VD : 4/5
4. muốn rút gọn phân số ta lấy cả tử vs mẫu chia cho 1 số nào đó
VD: \(\frac{10}{15}=\frac{10:5}{15:5}=\frac{2}{3}\)
a) \(A = \left\{ {a \in \mathbb{Z}| - 4 < a < - 1} \right\}\)
A là tập hợp các số nguyên a thỏa mãn \( - 4 < a < - 1\).
\( - 4 < a < - 1\) có nghĩa là: a là số nguyên nằm giữa \( - 4\) và \( - 1\). Có các số \( - 3; - 2\).
Vậy \(A = \left\{ { - 3; - 2} \right\}\)
b) \(B = \left\{ {b \in \mathbb{Z}| - 2 < b < 3} \right\}\)
B là tập hợp các số nguyên b thỏa mãn \( - 2 < b < 3\).
\( - 2 < b < 3\) có nghĩa là: b là số nguyên nằm giữa \( - 2\) và \(3\). Có các số \( - 1;0;1;2\).
Vậy \(B = \left\{ { - 1;0;1;2} \right\}\)
c) \(C = \left\{ {c \in \mathbb{Z}| - 3 < c < 0} \right\}\)
C là tập hợp các số nguyên c thỏa mãn \( - 3 < c < 0\).
\( - 3 < c < 0\) có nghĩa là: c là số nguyên nằm giữa \( - 3\) và 0. Có các số \( - 2; - 1\).
Vậy \(C = \left\{ { - 2; - 1} \right\}\)
d) \(D = \left\{ {d \in \mathbb{Z}| - 1 < d < 6} \right\}\)
D là tập hợp các số nguyên d thỏa mãn \( - 1 < d < 6\).
\( - 1 < d < 6\) có nghĩa là: b là số nguyên nằm giữa \( - 1\) và 6. Có các số \(0;1;2;3;4;5\).
Vậy \(D = \left\{ {0;1;2;3;4;5} \right\}\)
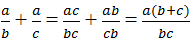
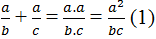
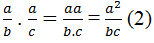
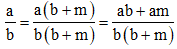
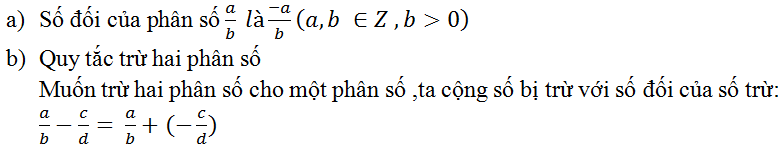
Số nghịch đảo của phân số \(\dfrac{a}{b}\)là phân số \(\dfrac{b}{a}\) ; (a ,b ∈ Z , a ≠ 0 , b ≠ 0)