Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(y'=\frac{-m-3}{\left(x-1\right)^2}\)
a) Vì \(x_0=0\Rightarrow y_0=-m-1;y'\left(x_0\right)=-m-3\)
Phương trình tiếp tuyến d của \(\left(C_m\right)\) tại điểm có hoành độ \(x_0=0\) là :
\(y=\left(-m-3\right)x-m-1\)
Tiếp tuyến đi qua \(A\) khi và chỉ khi \(3=\left(-m-3\right)4-m-1\Leftrightarrow m=-\frac{16}{5}\)
b) Ta có : \(x_0=2\Rightarrow y_0=m+5;y'\left(x_0\right)=-m-3\)
Phương trình tiếp tuyến \(\Delta\) của \(\left(C_m\right)\) tại điểm có hoành độ \(x_0=2\) là :
\(y=\left(-m-3\right)\left(x-2\right)+m+5=\left(-m-3\right)x+3m+11\)
* \(\Delta\cap Ox=A\Rightarrow A\left(\frac{3m+11}{m+3};0\right)\) với \(m+3\ne0\)
* \(\Delta\cap Oy=B\Rightarrow B\left(0;3m+11\right)\)
Suy ra diện tích tam giác OAB là : \(S=\frac{1}{2}OA.OB=\frac{1}{2}\frac{\left(3m+11\right)^2}{\left|m+3\right|}\)
Theo giả thiết bài toán suy ra \(\frac{1}{2}\frac{\left(3m+11\right)^2}{\left|m+3\right|}=\frac{25}{2}\)
\(\Leftrightarrow\left(3m+11\right)^2=25\left|m+3\right|\Leftrightarrow\)\(\left[\begin{array}{nghiempt}9m^2+66m+121=25m+75\\9m^2+66m+121=-25m-75\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}9m^2+41m+46=0\\9m^2+91m+196=0\end{array}\right.\Leftrightarrow\left[\begin{array}{nghiempt}m=-2;m=-\frac{23}{9}\\m=-7;m=-\frac{28}{9}\end{array}\right.\)

Với m = 1, ta có \(\left(C_1\right):y=\frac{x+1}{x-1}\)
a. Gọi d là đường thẳng đi qua P, có hệ số góc k => \(d:y=k\left(x-3\right)+1\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-3\right)+1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-3\right)+1\Leftrightarrow x=2\)
\(\Rightarrow k=-2\Rightarrow\) phương trình tiếp tuyến : \(y=-2x+7\)
b. Gọi d là đường thẳng đi qua A, có hệ số góc k : \(d:y=k\left(x-2\right)-1\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-2\right)-1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-2\right)-1\Leftrightarrow x=\pm\sqrt{2}\)
* \(x=\sqrt{2}\Rightarrow k=-2\left(3+2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3+2\sqrt{2}\right)x+11+8\sqrt{2}\)
* \(x=-\sqrt{2}\Rightarrow k=-2\left(3-2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3-2\sqrt{2}\right)x+11-8\sqrt{2}\)

a. Ta có : \(y'=3x^2-6x+2\)
\(x_0=1\Leftrightarrow y_0=-6\) và \(y'\left(x_0\right)=y'\left(-1\right)=11\)
Suy ra phương trình tiếp tuyến là \(y=y'\left(-1\right)\left(x+1\right)-6=11x+5\)
b. Gọi \(M\left(x_0;6\right)\) là tiếp điểm, ta có :
\(x_0^3-3x_0^2+2x_0=6\Leftrightarrow\left(x_0-3\right)\left(x_0^2+2\right)=0\Leftrightarrow x_0=3\)
Vậy phương trình tiếp tuyến là :
\(y=y'\left(3\right)\left(x-3\right)+6=11x-27\)
c. PTHD giao điểm của (C) với Ox :
\(x^3-3x^2+2x=0\Leftrightarrow x=0;x=1;x=2\)
* \(x=0\) ta có tiếp tuyến : \(y=y'\left(0\right)\left(x-0\right)+0=2x\)
* \(x=1\) ta có tiếp tuyến : \(y=y'\left(1\right)\left(x-1\right)+0=-x+1\)
* \(x=2\) ta có tiếp tuyến : \(y=y'\left(2\right)\left(x-2\right)+0=2x-4\)

Ta có \(y'=4x^3-16x\)
Vì \(x_0=1\Rightarrow y_0=m-6;y'\left(x_0\right)=-12\)
Phương trình tiếp tuyến d của \(\left(C_m\right)\) tại điểm có hoành độ \(x_0=1\) là :
\(y=-12\left(x-1\right)+m-6=-12x+m+6\)
Phương trình hoành độ giao điểm của \(\left(C_m\right)\) với d :
\(x^4-8x^2+m+1=-12x+m+6\Leftrightarrow x^4-8x^2+12-5=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^2+2x-5\right)=0\Leftrightarrow x=1,x=-1\pm\sqrt{6}\)
Vậy d và \(\left(C_m\right)\) luôn cắt nhay tại 3 điểm
\(A\left(1;m-6\right);B\left(-1\pm\sqrt{6};m+18\ne\sqrt{6}\right)\)

Giao điểm của đồ thị hàm số (C) và trục tung là điểm N(0;1)
Ta có : \(f'\left(x\right)=\frac{3}{\left(1-x\right)^2}\) suy ra tiếp tuyến tại điểm N là \(\left(\Delta\right):y=3x+1\Leftrightarrow\left(\Delta\right):3x-y+1=0\)
Xét điểm \(M\left(a+1;\frac{2a+3}{-a}\right)\in\left(C\right),a>0\)
Ta có : \(d_{M\\Delta }=\frac{\left|3\left(a+1\right)+\frac{2a+3}{a}+1\right|}{\sqrt{10}}=\frac{1}{\sqrt{10}}.\frac{3a^2+6a}{+3a}=\frac{3}{\sqrt{10}}\left(a+\frac{2}{a}+1\right)\ge\frac{3}{\sqrt{10}}\left(2\sqrt{2}+1\right)\)
Dấu bằng xảy ra khi \(a=\frac{2}{a}\Leftrightarrow a=\sqrt{2}\Rightarrow M\left(\sqrt{2}+1;\frac{2\sqrt{2}+5}{-\sqrt{2}}\right)\)

a. Tiếp tuyến của \(\left(C_m\right)\) tại điểm có hoành độ x = 1 có phương trình :
\(y=\left(m-2\right)\left(x-1\right)+3m-2=\left(m-2\right)x+3m\)
Yêu cầu của bài toán khi và chỉ khi \(\begin{cases}m-2=3\\2m\ne10\end{cases}\) vô nghiệm
Vậy không tồn tại m thỏa mãn yêu cầu bài toán
b. Ta có \(y'=3\left(x^2-\frac{4}{3}x+\frac{4}{9}\right)+m-\frac{7}{3}=3\left(x-\frac{2}{3}\right)^2+m-\frac{7}{3}\)
Suy ra \(y'\ge m-\frac{7}{3}\)
Tiếp tuyến tại điểm có hoành độ \(x=\frac{2}{3}\) có hệ số góc nhỏ nhất và hệ số góc có giá trị \(k=m-\frac{7}{3}\)
Yêu cầu bài toán \(\Leftrightarrow k.2=-1\Leftrightarrow\left(m-\frac{7}{3}\right).2=-1\Leftrightarrow m=\frac{11}{6}\)

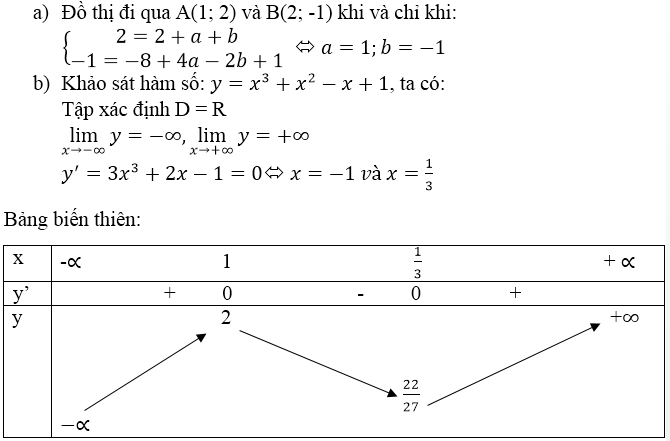
a) Tập xác định : D = R
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
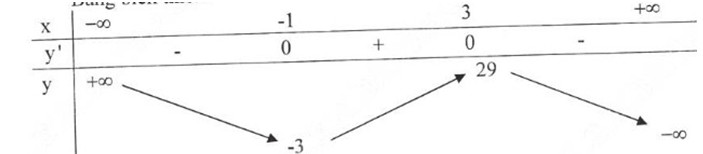
Đồ thị hàm số:
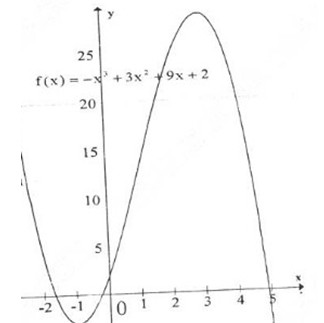
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6

b) Ta có \(y'=4x^3-4x;y\left(-2\right)=8;y'\left(-2\right)=-24\)
Phương trình tiếp tuyến phải tìm là :
\(y-y\left(-2\right)=y'\left(-1\right)\left(x+2\right)\)
\(\Leftrightarrow y-8=-24\left(x+2\right)\Leftrightarrow y=-24x-10\)
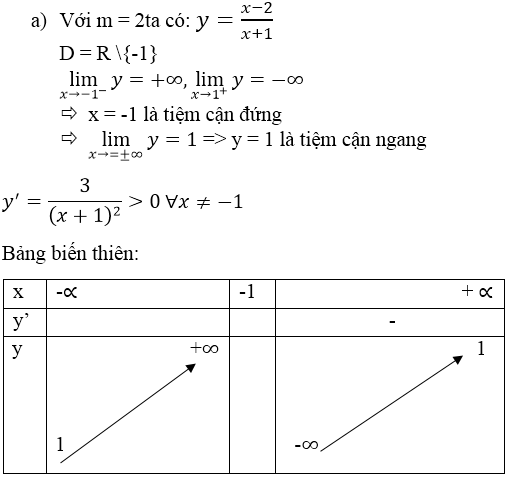
a: y'=3x^2-6
f(1)=1-6+5=0
f'(1)=3-6=-3
y-f(1)=f'(1)(x-1)
=>y-0=-3(x-1)
=>y=-3x+3
b: y=5
=>x^3-6x=0
=>x=0 hoặc x=căn 6 hoặc x=-6
TH1: x=0
y=5; y'=3*0^2-6=-6
Phương trình sẽ là:
y-5=-6(x-0)
=>y=-6x+5
TH2: x=căn 6
y=5; y'=3*6-6=12
Phương trình sẽ là:
y-5=12(x-căn 6)
=>y=12x-12căn 6+5
TH3: x=-căn 6
y=5; y'=12
Phương trình sẽ là:
y-5=12(x+căn 6)
=>y=12x+12căn 6+5