Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Gọi A (a; 0; 0), B(0; b; 0) và C(0; 0; c) với abc ≠ 0. Phương trình mặt phẳng (P) đi qua ba điểm A, B, C là
![]() .
.
Vì M(1;2;3) ∈ (P) nên ta có: ![]() .
.
Điểm M là trực tâm của tam giác ABC.
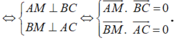

Phương trình mặt phẳng (P) là: ![]() <=> x + 3y + 2z - 14 = 0
<=> x + 3y + 2z - 14 = 0

Đáp án D
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC (M là trực tâm tam giác ABC) nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: n p → = OM → = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0

Đáp án D
Ta có OA ⊥ OB, OC => OA ⊥ (OBC) => OA ⊥ BC.
Mặt khác ta có AM ⊥ BC nên ta suy ra BC ⊥ (OAM) => BC ⊥ OM
Chứng minh tương tự ta được AC ⊥ OM. Do đó OM ⊥ (ABC).
Ta chọn n P → = OM → = (1; 2; 2). Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) + 2(y - 2) + 2(z - 2) = 0 <=> x + 2y + 2z - 9 = 0
Chọn D

Giả sử A(a;0;0); B(0;b;0) và C(0;0;c) với \(abc\ne0\). Khi đó, mặt phẳng (P) có phươn trình :
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
Do \(G\left(1;2;3\right)\in\left(P\right)\) nên
\(\frac{1}{a}+\frac{2}{b}+\frac{3}{c}=1\) (1)
Vì G là trọng tâm của tam giác ABC nên :
\(\begin{cases}1=\frac{a+0+0}{3}\\2=\frac{0+b+0}{3}\\3=\frac{0+0+c}{3}\end{cases}\)
Dễ dàng kiểm tra được \(a=3;b=6;c=9\) thỏa mãn (1). Vậy mặt phẳng cần tìm là \(\frac{x}{3}+\frac{y}{6}+\frac{z}{9}=1\)
hay \(6x+3y+2z-18=0\)

Đáp án B
Vì OA, OB, OC đôi một vuông góc và M là trực tâm tam giác ABC => OM ⊥ (ABC)
Suy ra mp(ABC) nhận O M → làm véc tơ pháp tuyến và đi qua điểm M(1;2;3)
Vậy phương trình mp(P):
![]()
<=> x +2y+3z -14=0

Chọn D
Vì A thuộc Ox nên A(a;0;0).
Vì B thuộc Oy nên B(0;b;0).
Vì C thuộc Oz nên C(0;0;c).
G là trọng tâm tam giác ABC khi và chỉ khi


Đáp án C
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c). Vì M(1;2;3) là trọng tâm của tam giác ABC nên ta có:
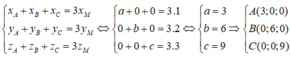
Vậy phương trình của mặt phẳng (P) là: x 3 + y 6 + z 9 = 1


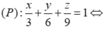
Do tứ diện OABC có OA, OB, OC đôi một vuông góc nên H là trực tâm của tam giác ABC khi và chỉ khi H là hình chiếu của O trên mặt phẳng (P).
Vậy mặt phẳng (P) đi qua H(1;2;1) và nhận vecto \(\overrightarrow{OH}=\left(1;2;1\right)\) làm vecto pháp tuyến suy ra (P) có phương trình :
\(1.\left(x-1\right)+2\left(y-2\right)+1\left(z-1\right)=0\)
hay \(x+2y+z-6=0\)
c