Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình của dao động điều hòa x= Acos(ωt + φ)
Trong đó :
- x : li độ của dao động (độ lệch của vật khỏi vị trí cân bằng) có đơn vị là centimet hoặc mét (cm ; m)
- A : biên độ dao động, có đơn vị là centimet hoặc mét (cm ; m)
- ω : tần số góc của dao động có đơn vị là radian trên giây (rad/s)
- (ωt + φ) : pha của dao động tại thời điểm t, có đơn vị là radian (rad)
- φ: pha ban đầu của dao động, có đơn vị là radian (rad)

Đáp án B
Phương pháp: Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác
Cách giải:
- Phương trình dao động của x; x1; x2: 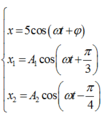
Suy ra :
+ Độ lệch pha giữa x và x1 là :![]()
+ Độ lệch pha giữa x và x2 là : 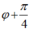
+ Độ lệch pha giữa x1 và x2 là : 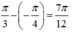
=> Ta có giản đồ vecto :
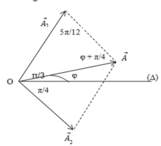
- Áp dụng định lí hàm số sin trong tam giác ta có:
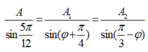
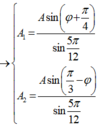
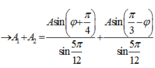
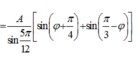
có: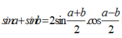
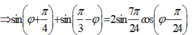
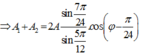
Để [A1 + A2] đạt cực đại thì 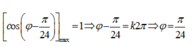

Chọn A
+ Các đại lượng A, ω và là hằng số (A và ω luôn dương)
+ từ đề thấy x phụ thuộc vào t theo dạng hàm số cos
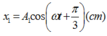
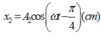

Phương tridnh dao động điều hòa là x = Acos(ωt+ Ø), trong đó:
- x là li độ của dao động
- A là biên độ dao động
- ω là tần số góc của đơn vị, có đơn vị là rad/s
- (ωt+ Ø) là pha của dao động tại thời điểm t, có đơn vị là rad,
- Ø là pha ban đầu của dao động
Phương trình dao động điều hòa
x=Acos(\(\omega\)t + \(\varphi\))
Trong đó x là li độ,
A là biên độ,
(\(\omega\)t + \(\varphi\)) là pha dao động (thường dùng đơn vị rad),
\(\varphi\) là pha ban đầu,
\(\omega\) là tần số góc (thường dùng đơn vị rad/s).