Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tiêu điểm có tọa độ \((4;0)\) nên ta có \(p = 8\)
Suy ra phương trình chính tắc của parabol là: \({y^2} = 16x\)
b) Đường chuẩn có phương trình \(x = - \frac{1}{6}\), nên ta có \(p = - \frac{1}{3}\)
Suy ra phương trình chính tắc của parabol có dạng \({y^2} = - \frac{2}{3}x\)
c) Gọi phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Thay tọa độ điểm \((1;4)\) vào phương trình \({y^2} = 2px\) ta có:
\({4^2} = 2p.1 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)
d) Gọi \(F\left( {\frac{p}{2};0} \right)\), \(\Delta :x + \frac{p}{2} = 0\) lần lượt là tiêu điểm và phương trình đường chuẩn của parabol ta có:
\(d\left( {F,\Delta } \right) = \frac{{\left| {\frac{p}{2} + \frac{p}{2}} \right|}}{1} = 8 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)

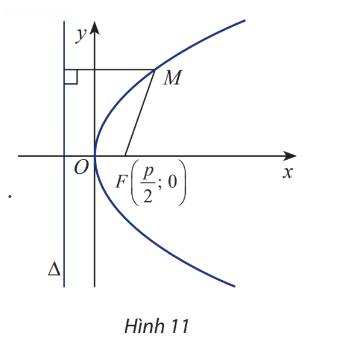
a) Ta có: \(\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} \)
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\)
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \)
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|\)

a) Ta có:
\(2p = \;\frac{5}{2} \Rightarrow p = \frac{5}{4} \Rightarrow \frac{p}{2} = \frac{5}{8}\).
Tiêu điểm của parabol là: \(F\left( {\frac{5}{8};0} \right)\)
Phương trình đường chuẩn là: \(x + \frac{5}{8} = 0\)
b) Ta có:
\(2p = 2\sqrt 2 \Rightarrow p = \sqrt 2 \Rightarrow \frac{p}{2} = \frac{{\sqrt 2 }}{2}\).
Tiêu điểm của parabol là: \(F(\frac{{\sqrt 2 }}{2};0)\)
Phương trình đường chuẩn là: \(x + \frac{{\sqrt 2 }}{2} = 0\)

a) Ta thấy phương trình có dạng \(a{x^2} + b{y^2} = 1\) nên phương trình \(({C_1}):4{x^2} + 16{y^2} = 1\) là phương trình của đường elip
Từ phương trình \(({C_1}):4{x^2} + 16{y^2} = 1\) ta có phương trình chính tắc là \(({C_1}):\frac{{{x^2}}}{{\frac{1}{4}}} + \frac{{{y^2}}}{{\frac{1}{{16}}}} = 1\)
Từ phương trình chính tắc ta có: \(a = \frac{1}{2},b = \frac{1}{4} \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{{\left( {\frac{1}{2}} \right)}^2} - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt 3 }}{4}\)
Suy ra tiêu điểm của elip này là \({F_1}\left( { - \frac{{\sqrt 3 }}{4};0} \right)\) và \({F_2}\left( {\frac{{\sqrt 3 }}{4};0} \right)\)
b) Ta thấy phương trình có dạng \(a{x^2} - b{y^2} = 1\) nên phương trình \(({C_2}):16{x^2} - 4{y^2} = 144\) là phương trình của đường hypebol
Từ phương trình \(({C_2}):16{x^2} - 4{y^2} = 144\) ta có phương trình chính tắc là \(({C_1}):\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{36}} = 1\)
Từ phương trình chính tắc ta có: \(a = 3,b = 6 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{3^2} + {6^2}} = 3\sqrt 5 \)
Suy ra tiêu điểm của hypebol này là \({F_1}\left( { - 3\sqrt 5;0} \right)\) và \({F_2}\left( {3\sqrt 5;0} \right)\)
c) Phương trình \(({C_3}):x = \frac{1}{8}{y^2}\) có dạng \({y^2} = ax\) nên phương trình này là phương trình của parabol
Ta có phương trình chính tắc là \({y^2} = 8x\)
Từ phương trình chính tắc ta có: \(2p = 8 \Rightarrow p = 4\)
Suy ra tiêu điểm là \(F(2;0)\)

a) Từ phương trình chính tắc \({y^2} = 12x\) ta có \(p = 6\)
Suy ra
+) Tiêu điểm của parabol \(F(3;0)\)
+) Phương trình đường chuẩn của parabol \(\Delta :x + 3 = 0\)
b) Từ phương trình chính tắc \({y^2} = x\) ta có \(p = \frac{1}{2}\)
Suy ra
+) Tiêu điểm của parabol \(F(\frac{1}{4};0)\)
+) Phương trình đường chuẩn của parabol \(\Delta :x + \frac{1}{4} = 0\)
Đáp án: B.
Ta có khoảng cách từ tiêu điểm đến đường chuẩn của một parabol bằng p ⇒ p = 2
Vậy phương trình chính tắc của parabol là: y 2 = 2.2x ⇔ y 2 = 4x