Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P: "\(\forall n \in \mathbb N,\;{n^2} \ge n".\)
Q: "\(\exists \;a \in \mathbb R,\;a + a = 0".\)

a) \(\exists a\in\mathbb{Z}:a=a^2\)
b) \(\forall x\in\mathbb{R}:x+0=x\)
c) \(\exists x\in\mathbb{Q}:x< \dfrac{1}{x}\)
d) \(\forall n\in\mathbb{N}:n>0\)

Mệnh đề P đúng, bình phương của một số thực luôn lớn hơn hoặc bằng 0 (không âm).
Mệnh đề Q sai vì \({x^2} = 2 \Leftrightarrow x = \pm \sqrt 2 \notin \mathbb Q\), do đó không có số hữu tỉ nào mà bình phương của nó bằng 2.

∀ x ∈ R : x + ( - x ) = 0 (đúng)
Phủ định là ∃ x ∈ R : x + ( - x ) ≠ 0 (sai)

a) An: "\(\forall x \in \mathbb R ,{x^2} \ge 0\)"
b) Bình: "\(\exists x \in ,{x^2} < 0\)"
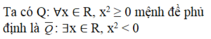
.