
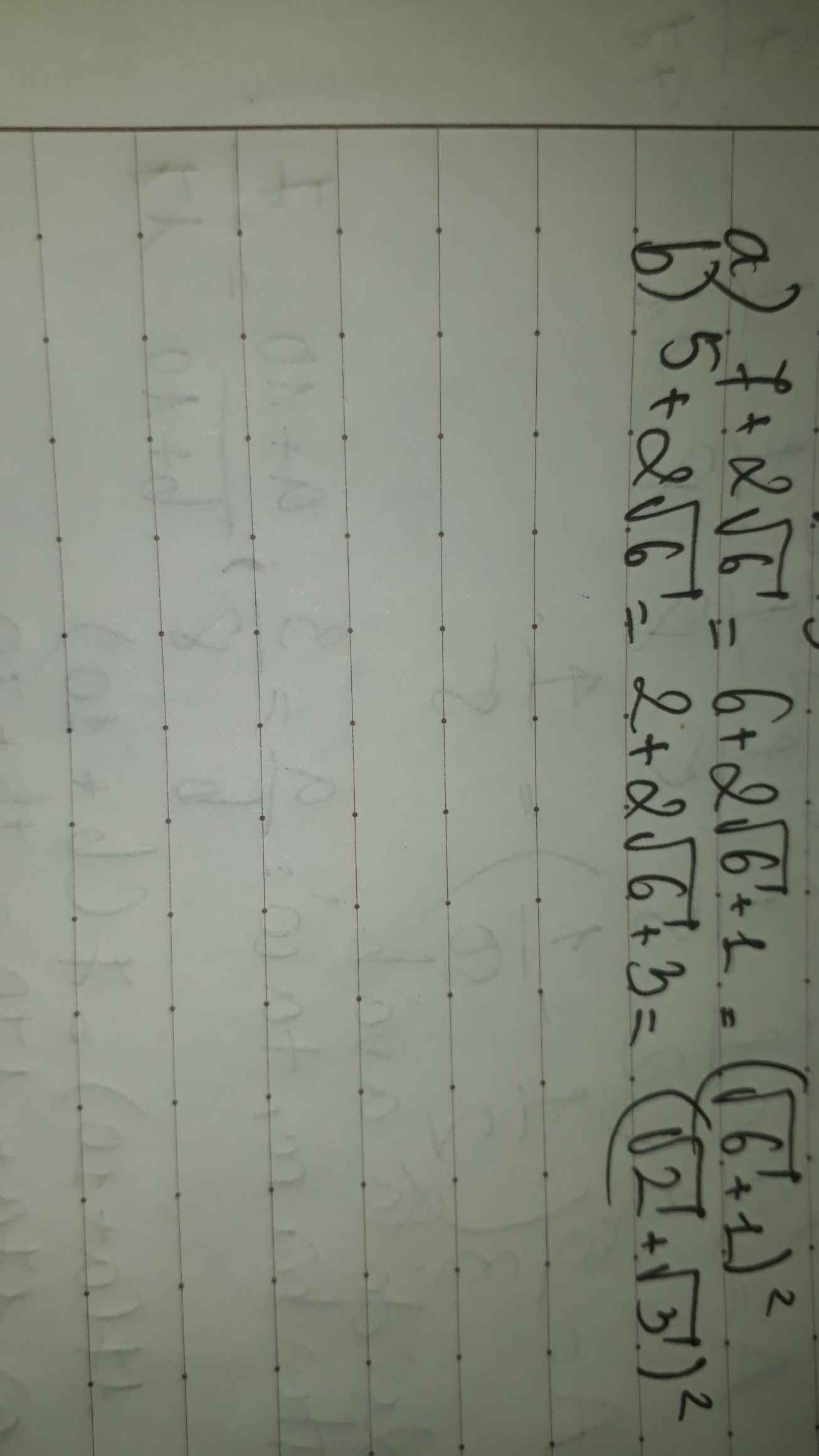
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

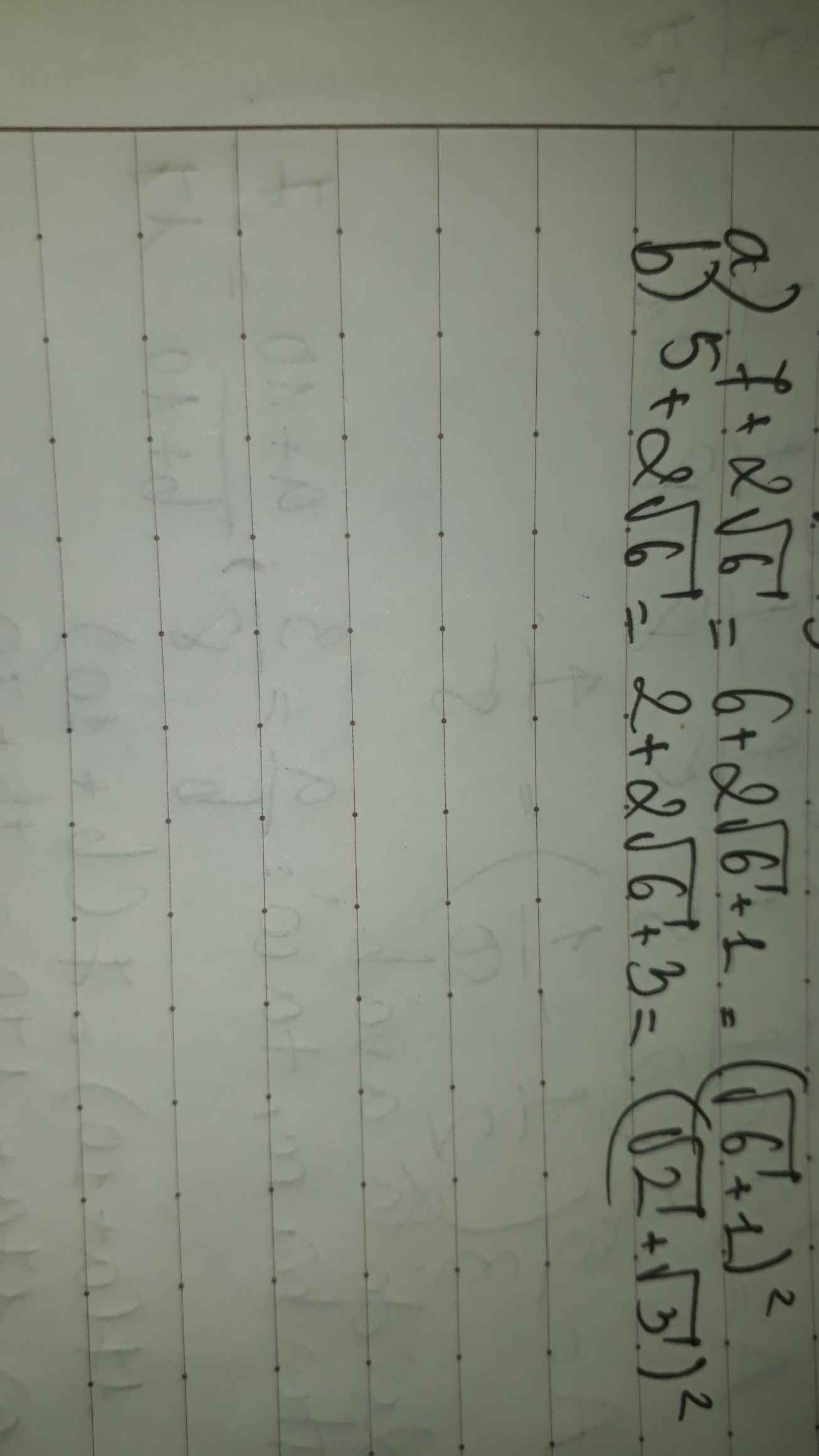







\(=\left(\frac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right).\frac{\left(x-1\right)^2}{2}\)
\(=\left(\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right).\frac{\left(x-1\right)^2}{2}\)
\(=\frac{\left(x-\sqrt{x}-2\right)-\left(x+\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}.\frac{\left(x-1\right)^2}{2}\)
\(=\frac{-2\sqrt{x}}{\left(x-1\right)\left(\sqrt{x}+1\right)}.\frac{\left(x-1\right)^2}{2}\)\(=\frac{-\sqrt{x}}{\sqrt{x}+1}.\left(x-1\right)=\frac{-x\sqrt{x}+\sqrt{x}}{\sqrt{x}+1}\)
\(=\left(\frac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right).\frac{\left(x-1\right)^2}{2}\)
\(=\left(\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right).\frac{\left(x-1\right)^2}{2}\)
\(=\frac{\left(x-\sqrt{x}-2\right)-\left(x+\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}.\frac{\left(x-1\right)^2}{2}\)
\(=\frac{-2\sqrt{x}}{\left(x-1\right)\left(\sqrt{x}+1\right)}.\frac{\left(x-1\right)^2}{2}\)\(=\frac{-\sqrt{x}}{\sqrt{x}+1}.\left(x-1\right)=\frac{-x\sqrt{x}+\sqrt{x}}{\sqrt{x}+1}\)

\(\left(1-\frac{5+\sqrt{5}}{1+\sqrt{5}}\right)\left(\frac{5-\sqrt{5}}{1-\sqrt{5}}-1\right)\)
\(=\left[1-\frac{\sqrt{5}\left(\sqrt{5}+1\right)}{1+\sqrt{5}}\right]\left[\frac{\sqrt{5}\left(\sqrt{5}-1\right)}{1-\sqrt{5}}-1\right]\)
\(=\left(1-\sqrt{5}\right)\left(-\sqrt{5}-1\right)=-\left(1-\sqrt{5}\right)\left(1+\sqrt{5}\right)=4\)