
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{A^2}=\left|A\right|\)
\(\sqrt{A_1\cdot A_2\cdot...\cdot A_n}=\sqrt{A_1}\cdot\sqrt{A_2}\cdot...\cdot\sqrt{A_n}\)(ĐK: \(A_1>=0;A_2>=0;...;A_n>=0\))
\(\sqrt{\dfrac{A}{B}}=\dfrac{\sqrt{A}}{\sqrt{B}}\left(A>=0;B>0\right)\)
\(\sqrt{\dfrac{A}{B}}=\sqrt{\dfrac{AB}{B^2}}=\dfrac{\sqrt{AB}}{B}\left(A>=0;B>0\right)\)
\(\sqrt{A^2\cdot B}=\left|A\right|\cdot\sqrt{B}\left(B>=0\right)\)
\(A\cdot\sqrt{B}=\left[{}\begin{matrix}\sqrt{A^2\cdot B}\left(A>=0\right)\\-\sqrt{A^2\cdot B}\left(A< 0\right)\end{matrix}\right.\)

\(a,\dfrac{5}{3\sqrt{8}}=\dfrac{5\sqrt{8}}{24};\dfrac{2}{\sqrt{b}}=\dfrac{2\sqrt{b}}{b}\\ b,\dfrac{5}{5-2\sqrt{3}}=\dfrac{5\left(5+2\sqrt{3}\right)}{13}=\dfrac{25+10\sqrt{3}}{12}\\ \dfrac{2a}{1-\sqrt{a}}=\dfrac{2a\left(1+\sqrt{a}\right)}{1-a}\\ c,\dfrac{4}{\sqrt{7}+\sqrt{5}}=\dfrac{4\left(\sqrt{7}-\sqrt{5}\right)}{2}=2\sqrt{7}-2\sqrt{5}\\ \dfrac{6a}{2\sqrt{a}-\sqrt{b}}=\dfrac{6a\left(2\sqrt{a}+\sqrt{b}\right)}{2a-b}=\dfrac{12a\sqrt{a}+6a\sqrt{b}}{2a-b}\)
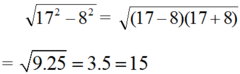
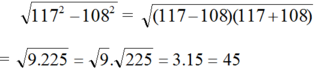
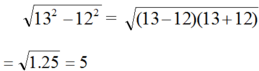
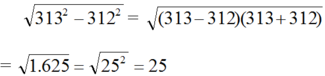
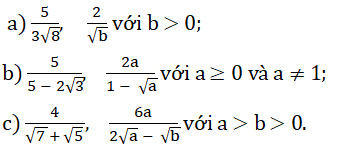
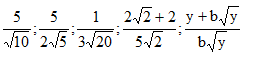
\(\sqrt{A^2}=\left|A\right|\)
\(\sqrt{AB}=\sqrt{A}\sqrt{B}\)
\(\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}\)
\(\sqrt{A^2B}=\left|A\right|\sqrt{B}\)
\(A\sqrt{B}=\sqrt{A^2B}\)
\(A\sqrt{B}=-\sqrt{A^2B}\)
\(\sqrt{\frac{A}{B}}=\frac{1}{\left|B\right|}\sqrt{AB}\)
\(\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}\)
\(\frac{C}{\sqrt{A}\pm B}=\frac{C\left(\sqrt{A}-+B\right)}{A-B^2}\)
\(\frac{C}{\sqrt{A}\pm\sqrt{B}}=\frac{C\left(\sqrt{A}-+\sqrt{B}\right)}{A-B}\)
1. \(\sqrt{A^2}=\left|A\right|\)
2. \(\sqrt{A.B}=\sqrt{A}.\sqrt{B}\left(A\ge0;b\ge0\right)\)
3. \(\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}\left(A\ge0;B\ge0\right)\)
4. \(\sqrt{A^2.B}=\sqrt{A^2}.\sqrt{B}=\left|A\right|.\sqrt{B}\left(B\ge0\right)\)
5. \(A\sqrt{B}\orbr{\begin{cases}\sqrt{A^2B}\left(A\ge0;B\ge0\right)\\\sqrt{A^2.B}\left(A< 0;B\ge0\right)\end{cases}}\)