HH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
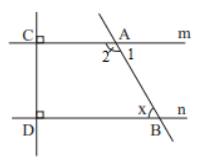
a) Vì m và n cùng vuông góc với CD nên m // n
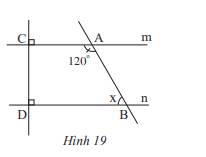
b) Ta có: \(\widehat {{A_2}} + \widehat {{A_1}} = 180^\circ \Rightarrow 120^\circ + \widehat {{A_1}} = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - 120^\circ = 60^\circ \)
Vì m // n nên \(\widehat {{A_1}} = \widehat {ABD}\) ( 2 góc so le trong) nên \(\widehat {ABD}\) = 60\(^\circ \)
Vậy x = 60\(^\circ \)
12 tháng 1 2023
Bài 1:
a=2b=3c
=>a/6=b/3=c/2
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{6}=\dfrac{b}{3}=\dfrac{c}{2}=\dfrac{a+b+c}{6+3+2}=\dfrac{180}{11}\)
=>a=1080/11; b=540/11; c=360/11
W
15 tháng 3 2020
a) Xét tam giác ABC. Ta có:
Vì AD là tia phân giác của góc A nên:
\(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{A}}{2}=40^{^o}\)
\(\widehat{ADB}=180^o-70^o-40^o=70^o\)
Vì \(\widehat{ADB}=\widehat{ABD}=70^o\)nên ABD là tam giác cân.
b)Vì \(\widehat{ADB}\)kề bù với \(\widehat{ADC}\)nên \(\widehat{ADC}=180^o-70^o=110^o\)
Do tam giác ACD là tam giác nên \(\widehat{ACD}=180^o-40^o-110^o=30^o\)
c) Đặt đỉnh ngoài của B là B1.
Ta có: \(\widehat{B_1}=180^o-70^o=110^o\)
LT
11 tháng 3 2020
A B C D
Vì tam giác ABC cân tại A suy ra AB = AC (T/c tam giác cân)
Mà AC = AD (GT)
suy ra AB = AD suy ra tam giác ABD cân tại A
b) Vì AB = AC = AD = 1/2AC nên AC = 2AB suy ra tam giác BDC vuông tại D
suy ra góc DBC = 90 độ
c) Để tam giác ABD đều suy ra góc ACB = 60 độ
28 tháng 4 2020
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
20 tháng 11 2021
a. Vì m⊥t và n⊥t nên m//n
b. Vì m//n nên \(\widehat{D}=\widehat{C_3}=75^0\) (so le trong)
Ta có \(\widehat{C_4}=180^0-\widehat{C_3}=105^0\) (kề bù)
20 tháng 11 2021
a) vì \(m\perp t\) mà \(n\perp t\)
=> m//n
b) vì m//n
=>\(D+C_4=180^O\\C_4 =180^O-D=105^O\)
D=C3=75o
24 tháng 1 2016
120o
day la san choi cua cac tai nang k biet thi dung tl tao lao
10 tháng 4 2022
a: Xét ΔDBC có
BA là đường trung tuyến
BA=DC/2
DO đó:ΔDBC vuông tại B
hay \(\widehat{DBC}=90^0\)
b: Vì ΔABD đều
nên \(\widehat{ABD}=60^0\)
=>\(\widehat{ABC}=30^0=\widehat{ACB}\)
21 tháng 7 2018
A B C D M
a) Xét hai tam giác AMB và tam giác DMC có:
MB = MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{CMD}\left(đ-đ\right)\)
MA = MD (gt)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c-g-c\right)\)
=> AB = CD (hai cạnh tương ứng)
b) Xét hai tam giác BMD và CMA có:
MB = MC (gt)
\(\widehat{BMD}=\widehat{CMA}\left(đ-đ\right)\)
MA = MD (gt)
\(\Rightarrow\Delta BMD=\Delta CMA\left(c-g-c\right)\)
\(\Rightarrow\widehat{MBD}=\widehat{MCA}\) (Hai góc tương ứng)
=> BD // AC
c) Ta có: AB vuông góc với AC (tam giác ABC vuông tại A)
BD // AC (cm ở câu b)
=> AB vuông góc với BD
=> \(\widehat{ABD}=90^0\)
VM
21 tháng 7 2018
A B C M D
a) Nối B và D lại
Xét tứ giác ABCD có
BM=MC (M là trung điểm của BC)
AM=MC (gt)
=>Tứ giác ABCD là hình bình hành
Do đó AB=CD
b)Ta có tứ giác ABCD là hình bình hành
=> BD // AC
c) Xét hình bình hành ABCD có
\(\widehat{A}=90^0\)
=>ABCD là hình chữ nhật
Vậy \(\widehat{ABD}=90^0\)
8 tháng 1 2022
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-80^0}{2}=50^0\)
b:\(\widehat{ABD}+\widehat{ABC}=180^0\)
\(\widehat{ACE}+\widehat{ACB}=180^0\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABD}=\widehat{ACE}\)
c: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE