Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vectơ ![]() cũng là vectơ chỉ phương của đường thẳng đã cho.
cũng là vectơ chỉ phương của đường thẳng đã cho.
Khi đó đường thẳng d có phương trình tham số:
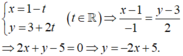
Chọn D

Đáp án C
Ta có: ![]()
Từ điểm D kẻ đường thẳng song song với AC, cắt cạnh AB tại điểm E. Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại F. Do AD là đường phân giác trong của tam giác ABC nên ta suy ra AEDF là hình thoi.
Đặt AE=AF=k. Ta có:
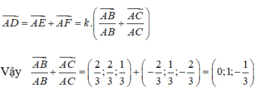
là một vectơ chỉ phương của đường thẳng AD. Từ đó suy ra C là khẳng định đúng.
Ta cũng lưu ý rằng khẳng định A sai, do tam giác ABC không cân tại đỉnh A.

ĐÁP ÁN A
Nếu u → là vectơ chỉ phương của một đường thẳng thì k u → (với k ≠ 0) đều là vectơ chỉ phương của đường thẳng đó.
Vì vậy các vectơ có tọa độ tỉ lệ với u → 2 ; - 3 đều là vectơ chỉ phương.
Ta có: 2 3 ≠ − 3 2 ; 2 − 2 = − 3 3 ; 2 6 = − 3 − 9 ; 2 − 4 = − 3 6
Do đó, trong các vecto đã cho có u 1 → không phải là vecto chỉ phương của đường thẳng ∆.

Khi phương trình đường thẳng cho dưới dạng tham số:
Thì đường thẳng có VTCP là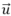 (a; b)
(a; b)
Do đó; phương trình đường thẳng đã cho có vecto chỉ phương là (6; 0)
(6; 0)
Lại có: vecto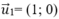 cùng phương với vecto
cùng phương với vecto 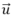 nên vecto
nên vecto 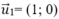 cũng là VTCP của đường thẳng đã cho.
cũng là VTCP của đường thẳng đã cho.
Chọn D.