Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B D E F C
Như hình vẽ trên: DE là pg góc ADB và DF là pg góc ADC
=>ADE = 1/2 (ADB) và ADF = 1/2(ADC)
=>ADE + ADF = EDF = 1/2(ADB + ADC) = 1/2*180 = 90
=>dpcm
Giải:
O x' x y t m 0 t' GT xOy và x'Oy kề bù Ot là tia phân giác của góc xOy Ot' là tia phân giác của góc x'Oy KL Ot vuông góc với Ot'
Đặt \(\widehat{xOy}=m^0(0< m^0< 180^0)\)
Hai góc xOy và yOx' là hai góc kề bù nên \(\widehat{xOy}+\widehat{yOx'}=180^0\)do đó \(\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-m^0\)
Theo giả thiết Ot và Ot' lần lượt là tia phân giác của góc xOy và x'Oy nên \(\widehat{tOy}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}m^0\)và \(\widehat{t'Oy}=\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\left[180^0-m^0\right]\). Tia Oy nằm giữa hai tia Ot và Ot', do đó \(\widehat{tOt}=\widehat{tOy}+\widehat{yOt'}=\frac{1}{2}m^0+\frac{1}{2}\left[180^0-m^0\right]=90^0\)
Vậy \(Ot\perp Ot'\)

trl:* tham khảo*
Góc bù nhau là 2 góc có tổng bằng 180 độ
Góc kề bù là hai góc kề nhau có tổng bằng 180 độ
Gó phụ nhau là có tổng hai góc bằng 90 độ
Gó kề nhau có tổng bằng 180 độ
và tổng hai góc phụ nhau bằng 90 đô
1. là 2 góc có tổng số đo = 180o
2. là 2 góc sát nhau
3. là 2 góc sát nhau có tổng số đo là 90o
4. là 2 góc vừa kề vừa bù
đúng ko mn

Bài 2:
A B D C 110
- Vì góc AOD đối đỉnh với góc COB:
nên \(COB=110^o\)
Vậy \(COB=110^o\)
- Vì góc AOD kề bù với góc AOC:
nên:\(AOD+AOC=180^o\)
hay:\(110^o+AOC=180^o\)
\(\Rightarrow AOC=180^o-110^o=70^o\)
Vậy \(AOC=70^o\)
- Vì AOC đối đỉnh với DOB:
nên: \(DOB=70^o\)
Vậy \(DOB=70^o\)
Bài 1: bạn xem lại bạn có ghi lộn ko nha ![]()
O A D C B
Trên hình vẽ có góc AOD đối đỉnh với góc BOC
góc AOB đối đỉnh với DOC
![]() mk giải cho bạn bài 1 rùi đó
mk giải cho bạn bài 1 rùi đó ![]()

Bài 2:
A B C D O
Vì AÔC và AÔD là 2 góc kề bù nên AÔC + AÔD=180o
Mà AÔC - AÔD =20o nên :
AÔC=(180+20):2 = 100 o ; mà AÔC đối đỉnh với góc BÔD nên BÔD = 100o
AÔD = 180-100=80o , mà AÔD đối đỉnh với góc BÔC nên BÔC = 80o
Bài 1:
A O B D C
Trước hết có các góc đối đỉnh bằng nhau là: AÔB = CÔD ; BÔC = AÔD
Và các góc bẹt bằng nhau : AÔC= BÔD

Gọi \(\widehat{xOz};\widehat{zOy}\) là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của \(\widehat{xOz;}\widehat{zOy}\).
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của \(\widehat{xOz};\widehat{zOy}\)
nên:
\(\widehat{uOz}\) = \(\frac{1}{2}\) \(\widehat{xOz}\)
\(\widehat{zOv}\) = \(\frac{1}{2}\) \(\widehat{xOy}\)
Suy ra:
\(2\widehat{uOz}=\widehat{xOz}\)
\(2\widehat{zOv}=\widehat{zOy}\)
Ta lại có:
\(\widehat{xOz}+\widehat{zOy}=180^0\)(vì 2 góc xOz, góc zOy kề bù)
\(\Rightarrow\) \(2\widehat{uOz}+2\widehat{zOv}=180^0\)
\(\Rightarrow\) \(2\left(\widehat{uOz}+\widehat{zOv}\right)=180^0\)
\(\Rightarrow\) \(\widehat{uOz}+\widehat{zOv}=90^0\)
\(\Rightarrow\) \(\widehat{uOv}=90^0\) (vì 2 \(\widehat{xOz};\widehat{zOy}\) kề nhau)
\(\Rightarrow\) Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

*Lời giải chi tiết:
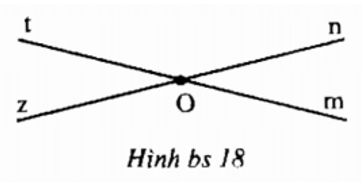
a) Vì góc nOt kề bù với góc mOn nên Ot là tia đối của tia Om. Tương tự, góc mOz kề bù với góc mOn nên Oz là hai tia đối của tia On. Từ đó, zOt và mOn là hai góc đối đỉnh.
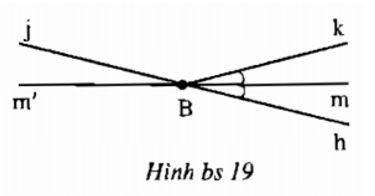
b) Vì góc kBj kề bù với góc hBk nên Bj là tia đối của tia Bh. Từ đó, m’Bj và hBm là hai góc đối đỉnh.
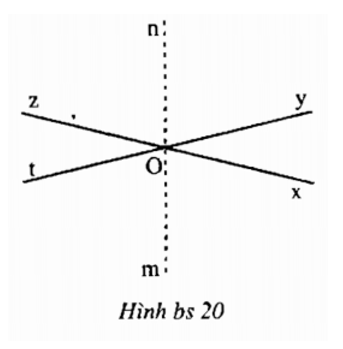
c) Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, zOy và tOx là hai góc đối đỉnh, tức là ∠zOy = ∠tOx.
Vì On, Om đều là tia phân giác và ∠zOy = ∠tOx nên ∠zOn = ∠nOy = ∠xOm = ∠mOt.
Lại vì ∠zOn + ∠nOx = 180°,
Nên ∠mOx + ∠nOx = 180°.
Suy ra Om và On là hai tia đối nhau.
Từ đó, ∠zOn và ∠mOx là hai góc đối đỉnh.

+) tia nam giua 2 tia
+)hai goc bang nhau
neu cac ban thay dung thi h cho minh nhe