Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu : ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
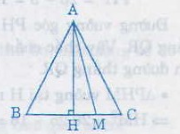
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC

B C A
tam giac ABC vuông tại A => AC\(^2\)= AB\(^2\)+AC\(^2\)( đinh lí Pyta-go )
AC^2>AB^2
Mà AB, AC >0
=> AC>AB
Vậy đường xiên lớn hơn đường vuông góc
hay đường vuông góc là nhỏ nhất

Theo hình vẽ các điểm A, B, C, D nằm trên một đường thẳng d và điểm M nằm ngoài đường thẳng đó. MA là đường vuông góc kẻ từ M đến đường thẳng d. Các đoạn thẳng MB, MC, MD là các đường xiên kẻ từ M lần lượt đến B, C và D
Ta có AB, AC, AD lần lượt là hình chiếu của MB, MC, MD xuống d. Ta có ngay AD >AC > AB suy ra
MD > MC >MB > MA
Điều đó có nghĩa là ngày hôm sau bạn Nam bơi đươci xa hơn ngày hôm trước, tức là bạn Nam tập đúng mục đích đề ra
Ngày hôm sau bạn Nam sẽ bơi được xa hơn ngày hôm trước. Vì MA lần lượt là hình chiếu của MB MC MD mà AB<AC<AD. Vậy Nam sẽ bơi được xa hơn ngày hôm trước

A B C H
a) XÉT tam giác HAC (\(\widehat{H}\)=\(90^O\)) CÓ
AH là đường vuông góc của hình xiên AC
\(\Rightarrow AC>AH\) (quan hệ giữa đường vuông góc và hình xiên trong tam giác) (đpcm)
b) Xét tam giác HAB (\(\widehat{H}=90^o\)) có
AH là đường vuông góc của đường xiên AB
\(\Rightarrow AB>AH\)(quan hệ giữa đường vuông góc và hình xiên) (đpcm)

Định lý 1
Trong một tam giác, góc đối diện với cạnh lớn hơn thi lớn hơn
Định lý 2
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Định lý 1: Trong một tam giác, góc đối diện với cạnh lớn hơn thi lớn hơn
Định lý 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
