Vẽ một tam giác vuông có một góc nhọn bằng \(40^0\) rồi viết các tỉ số lượng giác của góc...

\(40^0\) rồi viết các tỉ số lượng giác của góc...">

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

SG

Sách Giáo Khoa

26 tháng 4 2017

Vẽ một tam giác vuông có một góc nhọn bằng \(40^0\) rồi viết các tỉ số lượng giác của góc \(40^0\) ?

#Hỏi cộng đồng OLM #Toán lớp 9

1

NT

Nguyen Thuy Hoa

31 tháng 5 2017

Hệ thức lượng trong tam giác vuông

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

24 tháng 4 2017

Vẽ một tam giác vuông có một góc nhọn \(34^0\) rồi viết các tỉ số lượng giác của góc \(34^0\) ?

#Hỏi cộng đồng OLM #Toán lớp 9

3

NL

Nhật Linh

24 tháng 4 2017

Vẽ tam giác ABC vuông tại A, góc C = 34°

Theo định nghĩa ta có:

2016-11-05_162426

TT

Thien Tu Borum

24 tháng 4 2017

Hướng dẫn giải:

Vẽ tam giác ABC vuông tại A, $ˆC=34\circC^=34\circ$

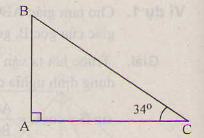
Theo định nghĩa ta có:

$sin34\circ=ABBCsin34\circ=ABBC$

$cos34\circ=ACBCcos34\circ=ACBC$

$tg34\circ=ABACtg34\circ=ABAC$

$cotg34\circ=ACABcotg34\circ=ACAB$ .

PT

Pham Trong Bach

31 tháng 1 2019

Vẽ một tam giác vuông có một góc nhọn bằng 40 ° rồi viết các tỉ số lượng giác của góc 40 °

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

31 tháng 1 2019

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

DP

Dung Phượng Ca

31 tháng 8 2017 - olm

2) Vẽ một tam giác vuông có một góc nhọn bằng 40 độ rồi viết các tỉ số lượng giác của góc 40 độ.

#Hỏi cộng đồng OLM #Toán lớp 9

2

HH

Huy Hoang

16 tháng 7 2020

c a b A B C 40 o

Vẽ tam giác ABC vuông tại A có \(\widehat{B}=90^o\)

Đặt AB = p ; AC = n ; BC = m

Ta có : \(sin40^o=sin\widehat{B}=\frac{AC}{BC}=\frac{n}{m}\)

\(cos40^o=cos\widehat{B}=\frac{AB}{BC}=\frac{p}{m}\)

\(tg40^o=tg \widehat{B } =\frac{AC}{AB}=\frac{n}{p}\)

\(cotg40^o=cotg \widehat{B} =\frac{AB}{AC}=\frac{p}{n}\)

LT

Lê Thanh Tâm

23 tháng 9 2021

Vẽ ∆ góc C = 40° Góc A = 90° → Góc B = 50° GIẢI Tỉ số lượng giác của góc 40° là Sin = AC/BC Cos = AB/BC Tg = AC/AB Cot = AB/AC

SG

Sách Giáo Khoa

27 tháng 4 2017

Trong tam giác vuông có một cạnh góc vuông bằng b, góc nhọn kề với nó bằng \(\alpha\)

a) Hãy biểu thị cạnh góc vuông kia, góc nhọn kề với cạnh này và cạnh huyền qua b và \(\alpha\)

b) Hãy tìm các giá trị của chúng khi \(b=12cm,\alpha=42^0\) (làm tròn kết quả đến chữ số thập phân thứ ba)

#Hỏi cộng đồng OLM #Toán lớp 9

1

NT

Nguyen Thuy Hoa

1 tháng 6 2017

Hệ thức lượng trong tam giác vuông

SG

Sách Giáo Khoa

24 tháng 4 2017

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn \(45^0\):

\(\sin60^0;\cos75^0;\sin52^030';cotg82^0;tg80^0\)

#Hỏi cộng đồng OLM #Toán lớp 9

3

NL

Nhật Linh

24 tháng 4 2017

Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:

sin60° = cos(90° – 60°) = cos30°

Tương tự:

cos75° = sin(90° – 75°) = sin 15°

sin52°30′ = cos(90° – 52°30′) = 38°30′

cotg82° = tg8°; tg80° = cotg10°

LH

Lưu Hạ Vy

24 tháng 4 2017

Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:

\(sin60^0=cos\left(90^0-60^0\right)=cos30^0\)

\(cos75^0=sin15^0;sin52^030'=cos37^030'\)

\(cotg82^0=tg8^0;tg80^0=cotg10^0\)

HD

Hoàng Đình Đại

10 tháng 10 2018 - olm

a) cho tam giác ABC có \(\widehat{B}=40^0,\widehat{C}=30^0\). dựng điểm D khác phía với B sao cho \(\widehat{DAC}=\widehat{DCA}=50^0\)

Chứng minh rằng tam giác ABC cân.

b) chứng minh rằng chu vi một tam giác có các góc nhọn hơn 4 lần bán kính đường tròn ngoại tiếp tam giác.

#Hỏi cộng đồng OLM #Toán lớp 9

2

I

Inequalities

27 tháng 2 2020

câu a) mình nghĩ chứng minh ABD cân chứ ạ, sao lại ABC

KN

Kiệt Nguyễn

27 tháng 2 2020

Gọi H là trung điểm của AC. \(\Delta\)DAC cân tại D.

Do đó DH\(\perp\)AC và AH = \(\frac{1}{2}\)AC (1)

Vẽ AK \(\perp\)BC. Vì \(\Delta\)AKC vuông tại K và ^BCA = 30⁰

nên AK = \(\frac{1}{2}\)AC (2)

Từ (1) và (2) suy ra AK = AH

Xét \(\Delta\)AKB và \(\Delta\)AHD có:

^AKB = ^AHD (=90⁰)

AK = AH(gt)

^BAK = ^DAH (=50⁰)

Do đó \(\Delta\)AKB = \(\Delta\)AHD (g.c.g)

=> AB = AD

Vậy \(\Delta\)ABD cân tại A(đpcm)

LH

Lê Hồng Nhung

23 tháng 7 2016 - olm

1) Cho tam giác ABC vuông tại A. Từ điểm D trên cạnh AC, vẽ DE vuông góc với BC tại E. Chứng minh \(\sin B\)=\(\frac{AB.AD+EB.ED}{AB.EB+AD.ED}\)2) Cho tam giác ABC có 3 góc nhọn, AB=c, AC=b,BC-a. Chứng minh rằng \(^{a^2=b^2+c^2-2bc.\cos A}\)3) Tính các tỉ số lượng giác sau ( không dùng bảng lượng giác và máy tính):a) \(\tan15^o,\sin15^o\)b) \(\sin22^o30',\tan22^o30'\)c)...

#Hỏi cộng đồng OLM #Toán lớp 9

0

LT

Le Trang Nhung

19 tháng 3 2017 - olm

Tỉ số giữa bán kính của đường tròn ngoại tiếp và bán kính của đường tròn nội tiếp tam giác vuông có góc nhọn bằng \(30^0\) là

#Hỏi cộng đồng OLM #Toán lớp 9

1

TA

Thiên An

2 tháng 5 2017

Gọi cạnh huyền là a, cạnh đối diện góc 30⁰ là c, cạnh còn lại là b

Tính được \(b=c.\cot30=c\sqrt{3}\) nên \(a=\sqrt{b^2+c^2}=\sqrt{\left(c\sqrt{3}\right)^2+c^2}=2c\)

Bán kính đường tròn ngoại tiếp là R = a/2 = 2c/2 = c

Bán kính đường tròn nội tiếp là

\(r=\frac{S}{p}=\frac{bc}{2p}=\frac{bc}{a+b+c}=\frac{c^2\sqrt{3}}{2c+c\sqrt{3}+c}=\frac{c^2\sqrt{3}}{\left(3+\sqrt{3}\right)c}=\frac{\left(\sqrt{3}-1\right)c}{2}\)

Do đó \(\frac{R}{r}=c.\frac{2}{\left(\sqrt{3}-1\right)c}=1+\sqrt{3}\)

bạn thi vio à kết bạn vs mk nhé

SG

Sách Giáo Khoa

26 tháng 4 2017

Cạnh góc vuông kề với góc \(60^0\) của một tam giác vuông bằng 3. Sử dụng bảng lượng giác của các góc đặc biệt, hãy tìm cạnh huyền và cạnh góc vuông còn lại (làm tròn đến chữ số thập phân thứ tư) ?

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

16 tháng 5 2022

Xét ΔABC vuông tại A có

\(AC=AB\cdot\tan60^0=3\sqrt{3}\simeq5,1962\left(cm\right)\)

=>\(BC=\sqrt{AB^2+AC^2}=6\left(cm\right)\)