Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

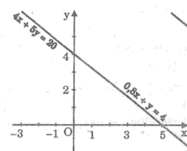
*Ta có: 4x + 5y = 20 ⇔ y = -0,8x + 4
Cho x = 0 thì y = 4 ⇒ (0; 4)
Cho y = 0 thì x = 5 ⇒ (5; 0)
*Ta có: 0,8x + y = 4 ⇔ y = -0,8x + 4
Vậy hai đường thẳng trùng nhau nên chúng có vô số điểm chung.
Đồ thị:

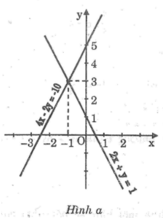
*Ta có: 2x + y = 1 ⇔ y = -2x + 1
Cho x = 0 thì y = 1 ⇒ (0; 1)
Cho y = 0 thì x = 1/2 ⇒ (1/2 ; 0)
*Ta có: 4x – 2y = -10 ⇔ y = 2x + 5
Cho x = 0 thì y = 5 ⇒ (0; 5)
Cho y = 0 thì x = - 5/2 ⇒ (- 5/2 ; 0)
Hoành độ giao điểm của hai đường thẳng:
-2x + 1 = 2x + 5 ⇔ 4x = -4 ⇔ x = -1
Tung độ giao điểm của hai đường thẳng:
y = -2(-1) + 1 = 2 + 1 = 3
Vậy tọa độ giao điểm của hai đường thẳng là (-1; 3).
Đồ thị:

(đơn vị đo trên các trục tọa độ là xentimet)
Lời giải:
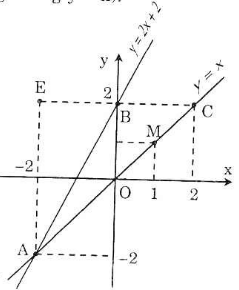
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x. Vẽ đường thẳng qua B(0; 2) và E(-1; 0) được đồ thị hàm số y = 2x + 2.
b) Tìm tọa độ của điểm A: giải phương trình 2x + 2 = x, tìm được x = -2. Từ đó tìm được x = -2, từ đó tính được y = -2, ta có A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
a) Đồ thị hàm số \(y=x\) là 1 đường thẳng đi qua 2 điểm O \(\left(0;0\right)\) và E\(\left(1;1\right)\)
Đồ thị hàm số \(y=2x+2\) là 1 đường thẳng đi qua 2 điểm B \(\left(0;2\right)\) và D \(\left(-1;0\right)\)
b) Hoành độ giao điểm A của 2 đường thẳng đã cho là nghiệm của pt:
\(x=2x+2\)
\(\Leftrightarrow\) \(x-2x=2\)
\(\Leftrightarrow\) \(-x=2\)
\(\Leftrightarrow\) \(x=-2\)
Tại \(x=-2\) thì giá trị của y là: \(y=2.\left(-2\right)+2=-2\)
Vậy tọa độ điểm A \(\left(-2;-2\right)\)
c) Đường thẳng song song với trục tung Ox và cắt trục hoành tại điểm B(0;2)
\(\Rightarrow\) Suy ra phương trình đường thẳng có dạng \(y=2x\)
Hoành độ giao điểm C của 2 đường thẳng y=2x và y=x là nghiệm của pt: 2x=x
\(\Rightarrow\) Tọa độ điểm C (2;2)
\(S_{ABC}=S_{ADO}+S_{BCOD}\)

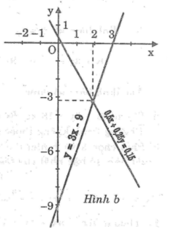
*Ta có: 0,5x + 0,25y = 0,15 ⇔ y = -2x + 0,6
Cho x = 0 thì y = 0,6 ⇒ (0; 0,6)
Cho y = 0 thì x = 0,3 ⇒ (0,3; 0)
*Ta có: 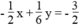 ⇔ y = 3x – 9
⇔ y = 3x – 9
Cho x = 0 thì y = -9 ⇒ (0; -9)
Cho y = 0 thì x = 3 ⇒ (3; 0)
Hoành độ giao điểm của hai đường thẳng:
-2x + 0,6 = 3x – 9 ⇔ 5x = 9,6 ⇔ x = 1,92
Tung độ giao điểm của hai đường thẳng:
y = 3.1,92 – 9 = -3,24
Vậy tọa độ giao điểm của hai đường thẳng là (1,92; -3,24)
Đồ thị:

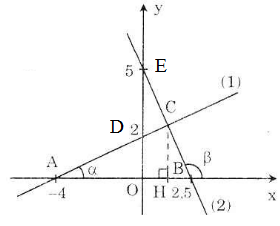
a) * Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0, tính được y = 2 => D(0; 2) thuộc đồ thị.
Cho y = 0, 0 = 0,5.x + 2 => x = -4 => A(-4; 0) thuộc đồ thị. Đường thẳng vẽ qua A, D là đồ thị của (1).
*Vẽ đồ thị hàm số y = 5 – 2x (2)
-Cho x = 0 tính được y = 5 E(0; 5) thuộc đồ thị
-Cho y = 0, 0 = 5 – 2x => x = 2,5 => B(2,5; 0) thuộc đồ thị. Đường thẳng vẽ qua B, E là đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)

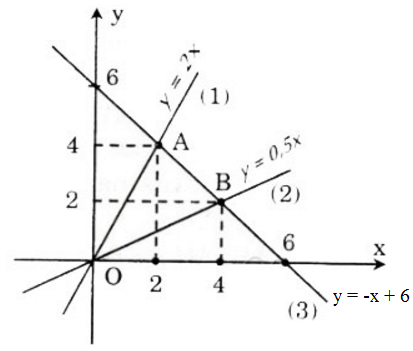
a) – Vẽ đường thẳng (1) qua gốc tọa độ O và điểm (1; 2)
-Vẽ đường thẳng (2) qua gốc tọa độ O và điểm (1; 0,5)
-Vẽ đường thẳng (3) qua hai điểm (0; 6) và (6; 0).
b) Gọi A, B theo thứ tự là giao điểm của đường thẳng (3) với các đường thẳng (1) và (2), ta có:
- x + 6 = 2x => x = 2 => y = 4 => A(2; 4)
- x + 6 = 0,5x => x = 4 => y = 2 => B(4; 2)

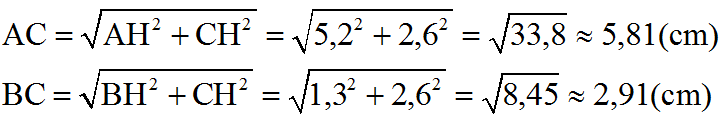


*Ta có: 4x + 5y = 20 ⇔ y = -0,8x + 4
Cho x = 0 thì y = 4 ⇒ (0; 4)
Cho y = 0 thì x = 5 ⇒ (5; 0)
*Ta có: 2x + 2,5y = 5 ⇔ y = -0,8x + 2
Cho x = 0 thì y = 2 ⇒ (0; 2)
Cho y = 0 thì x = 2,5 ⇒ (2,5; 0)
Hai đường thẳng có hệ số góc bằng nhau nhưng hệ số tự do khác nhau nên chúng song song với nhau. Suy ra chúng không có giao điểm chung.
Đồ thị: