Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

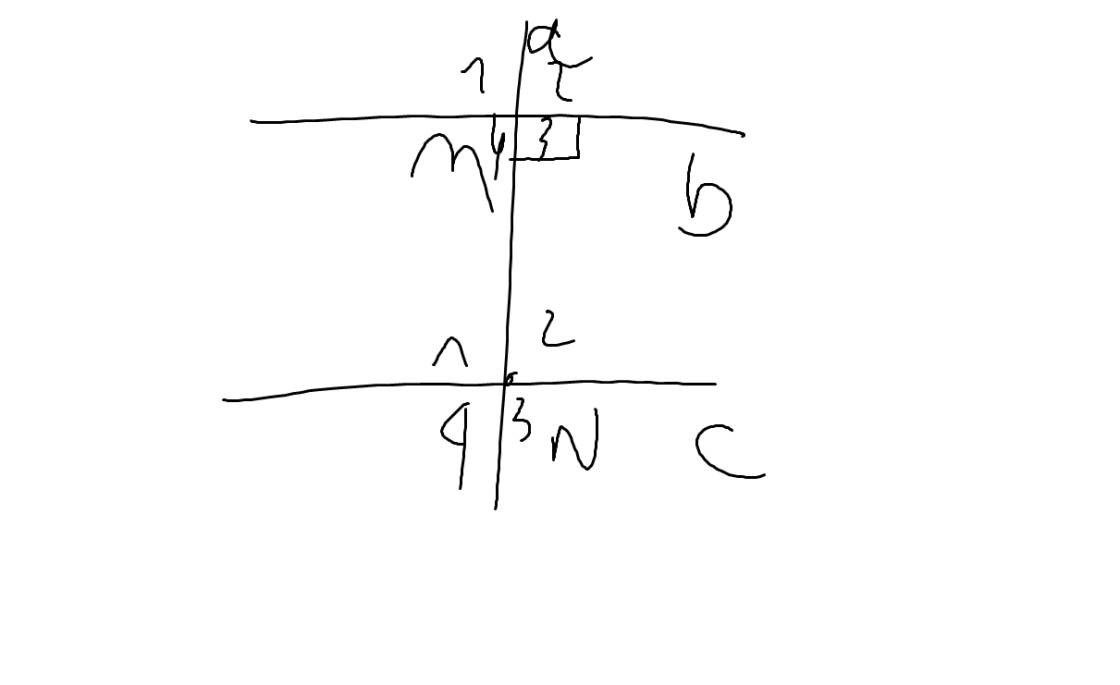
| GT | a\(\perp\)b tại M a cắt c tại N b//c |
| KL | a\(\perp\)c tại N |
Chứng minh định lí:
Ta có: b//c
=>\(\widehat{M_3}=\widehat{N_1}\)(hai góc so le trong)
mà \(\widehat{M_3}=90^0\)
nên \(\widehat{N_1}=90^0\)
=>a\(\perp\)c tại N

Vẽ hình thì dựa theo trong sách có nhé bạn!
a/ Bài a của bạn mình đọc không hiểu lắm hình như viết sai đề phải không bạn?
b/ GT: a song song với b,
c vuông góc với a
KL: c vuông góc với b
CẢM ƠN ĐÃ ĐỌC ĐÁP ÁN CỦA MÌNH

a) Giả thiết : Nếu 1 đường thẳng cắt 1 trong 2 dường thẳng song song
Kết luận: thì nó cắt đường thẳng kia
b) Giả thiết : Nếu 1 đường thẳng vuông góc với 1 trong hai đường thẳng song song
Kết luận : thì nó cũng vuông góc với đường thẳng kia
CHÚC BẠN HỌC TỐT NHA !

Bài 1:
| GT | a\(\perp\)b;b\(\perp\)c |
| KL | a//c |
Ta có: a\(\perp\)b
b\(\perp\)c
Do đó: a//c(Định lí 1 từ vuông góc tới song song)
Bài 2:
| GT | a\(\perp\)b;b//c |
| KL | a\(\perp\)c |
Ta có: b//c
a\(\perp\)b
Do đó: a\(\perp\)c


Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b.
Thật vậy,
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) ( 2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \)nên \(\widehat {{B_1}} = 90^\circ \) hay \(b \bot c\)(đpcm)

vẽ hình thì cậu tự vẽ nhé thì 2 đường thẳng song song gọi là a và b.Còn đường vuông góc gọi là c
GT:
- a vuông góc với c
- a song song với b
KL:
- b vuông góc với c
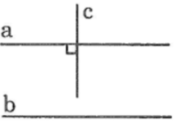

a b c M N
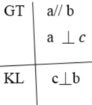
GT: a//b; \(c\perp a\)
KL: \(c\perp b\)
CM:
\(c\perp a\left(gt\right)\Rightarrow\widehat{cMa}=90^o\)
a//b \(\Rightarrow\widehat{cNb}=\widehat{cMa}=90^o\) (góc đồng vị) \(\Rightarrow c\perp b\)