K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
SG
1

5 tháng 10 2017
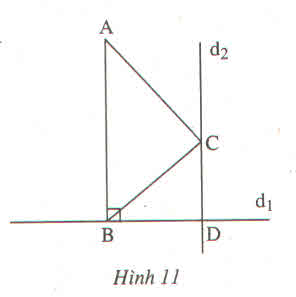
- Vẽ ∆ABC
- Vẽ đường thẳng d1 đi qua B và vuông góc với AB
- Vẽ đường thẳng d2 đi qua C và vuông góc với AB
- Gọi D là giao điểm của d1 và d2
Câu hỏi: Tại sao BDC=90o?

MH
26 tháng 5 2017
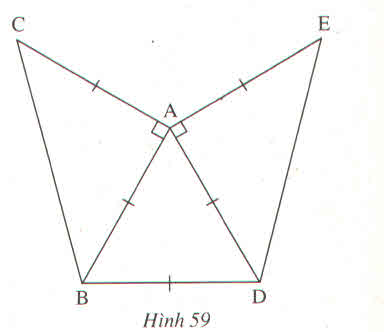
Đặt đề : Vẽ tam giác đều ABC . Vẽ tam giác ABD vuông cân tại B(D và C nằm khác phía đối với AB)
Vẽ tam giác ACE vuông cân tại C ( E và B nằm khác phía đối với AC )
Đo góc DAE = 150o