Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O 1 2 3
| Giả thiết | Góc O1 và góc O3 đối đỉnh |
| Kết luận | Góc O1 = Góc O3 |
C/m :
Ta có :
\(\begin{cases}\widehat{O_1}+\widehat{O_2}=180^0\\\widehat{O_3}+\widehat{O_2}=180^0\end{cases}\) ( kề bù )
\(\Rightarrow\begin{cases}\widehat{O_1}=180^0-\widehat{O_2}\\\widehat{O_3}=180^0-\widehat{O_2}\end{cases}\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}\left(đpcm\right)\)

GT KL đường thẳng a;b cắt nhau tại O góc O 1 và O 2 đối đỉnh góc O góc O 1 = 2 a b O 1 2 3
Vì góc O1 và góc O2 kề bù => O1 + O2 = 180o
Góc góc O2 và góc O3 kề bù => O2 + O3 = 180o
=> O1 = O2

\(\frac{3x-y}{x+y}=\frac{3}{4}\)
\(\Leftrightarrow4\left(3x-y\right)=3\left(x+y\right)\)
\(\Leftrightarrow12x-4y=3x+3y\)
\(\Leftrightarrow12x-4y-3x-3y=0\)
\(\Leftrightarrow9x-7y=0\)
\(\Leftrightarrow9x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{9}\)

a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |

a)
b)
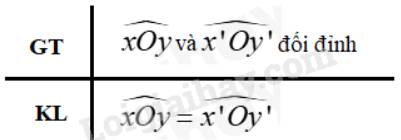
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)

Bài 1:
a)Chúng cùng tù hoặc cùng nhọn( giả thiết )
Chúng bằng nhau( kết luận )
b) Góc này nhọn, góc kia tù ( giả thiết )
Chúng bù nhau ( kết luận )
Bài 2:
a)( hình trên ) Chúng cùng tù cùng nhọn( Giả thiết)
Chúng bằng nhau ( kết luận )
b) Góc này nhọn, góc kia tù ( giả thiết )
Chúng bù nhau ( kết luận )
Giả Thiết 2 góc đối đỉnh Kết Luận Thì bằng nhau
Giả thuyết Kết luận 2 góc đối đỉnh Bằng nhau