Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
=>HC=HD
Xét ΔBCD có
BH vừa là đường cao, vừa là đường trung tuyến
Do đó: ΔBCD cân tại B
=>BC=BD
b: ΔOCD cân tại O
mà OH là đường cao
nên OH là phân giác của góc COD
c: góc ICA=1/2*sđ cung CA
góc OBC=góc ABC=1/2*sđ cung CA
Do đó: góc ICA=góc OBC
Xét ΔOCI và ΔODI có
OC=OD
góc COI=góc DOI
OI chung
Do đó: ΔOCI=ΔODI
=>góc OCI=góc ODI=90 độ
=>ID vuông góc DO

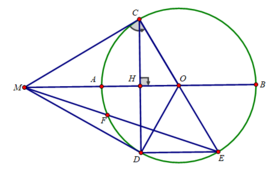
b) Ta có: OM = OA + AM = R + R = 2R
Xét tam giác MCO vuông tại C, CH là đường cao có:
MO 2 = MC 2 + OC 2
![]()
CH.OM = CM.CO
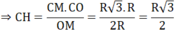
Lại có: CD = 2CH ⇒ CD = R 3
Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D
Theo định lí Py ta go ta có:
CE 2 = CD 2 + DE 2
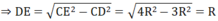

a) Xet tam giac COA can tai O( OA= OC) co CI vua la duong cao vua la trung tuyen ung voi AO nen tam giac OAC deu. Suy ra goc COA bang 60do , suy ra so do cung CA bang 60do. Suy ra goc COB bang 180-60=120 suy ra so do cung CA bang 120. Co: HCA=1/2sd cungCA=60/2=30 (1)
Co goc CHB=1/2(sd cungCB- sd cungCA) =1/2(120-60)=1/2*60=30 (2)
Tu (1); (2) suy ra: tam giac ACH can tai A. Suy ra AC= AH (3)
Lai co: tam giac CAO deu nen CA= CO (4)
Tu (3);(4)suy ra CA=CO=AH⏩ tam giac CHO vuong tai C
➡CO vuong goc voi HC tai C
Vay HC la tiep tuyen
b). Tu giac ACOD la hinh thoi
Tu giac co 4 canh ( CA= CO=OD=DA) bang nhau
c).

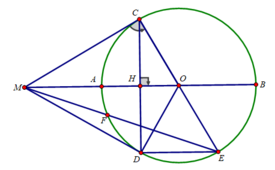
d) Ta có: ∠(CFE) = 90 0 (F thuộc đường tròn đường kính CE)
Lại có CF là đường cao nên MC 2 = MF.ME
Tương tự, ta có: MC 2 = MH.MO
⇒ ME.MF = MH.MO
⇒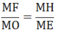
Xét ΔMOF và ΔMEN có:
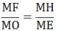
∠(FMO) chung
⇒ ΔMOF ∼ ΔMEN (c.g.c)
⇒ ∠(MOF) = ∠(MEH)

a: Xét ΔCOB có
CI là đường cao
CI là đường trung tuyến
Do đó: ΔCOB cân tại C
mà OC=OB
nên ΔCOB đều
=>\(\widehat{COB}=60^0=\widehat{CBA}\)
Xét ΔOCE vuông tại C có \(cosCOB=\dfrac{OC}{OE}\)
=>\(\dfrac{R}{OE}=\dfrac{1}{2}\)
=>OE=2R
b:
ΔOCE vuông tại C
=>\(\widehat{COE}+\widehat{CEO}=90^0\)
=>\(\widehat{CEO}=90^0-60^0=30^0\)
ΔOCD cân tại O
mà OE là đường cao
nên OE là phân giác của góc COD
Xét ΔOCE và ΔODE có
OC=OD
\(\widehat{COE}=\widehat{DOE}\)
OE chung
Do đó: ΔOCE=ΔODE
=>\(\widehat{CEO}=\widehat{DEO}=30^0\)
=>\(\widehat{CED}=60^0\)
Xét ΔECD có
EI là đường cao
EI là trung tuyến
Do đó: ΔECD cân ạti E
=>EC=ED
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>\(\widehat{CAB}+\widehat{CBA}=90^0\)
=>\(\widehat{CAB}=90^0-60^0=30^0\)
Xét ΔCAE có \(\widehat{CAE}=\widehat{CEA}=30^0\)
nên ΔCAE cân tại C
ΔCAE cân tại C
mà CI là đường cao
nên I là trung điểm của AE
Xét tứ giác ACED có
I là trung điểm chung của AE và CD
nên ACED là hình bình hành
mà EC=ED
nên ACED là hình thoi
c: ΔOCE=ΔODE
=>\(\widehat{ODE}=\widehat{OCE}=90^0\)
=>ED là tiếp tuyến của (O)