Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu a,ABCDH HBC=>AD=BC mà ,F là trung điểm BC,AD=>À=BE1
=>AD//BC MÀ F thuộc AD,E thuộc BC
=>AB//FE2
1,2=>ABEF HBH
MIK K BT ĐÚNG K NX LM NGƠ xl bn nha vì mik ms hc lp 6

a ,
Ta có BE//AD => ABED là hình thang
xét tam giác CED có EC=DC và có góc C=60°
=>CED là tam giác đều
=>EDC=60°
ta có BDE=D-ECD (đây là ký hiệu góc)
=>BDE=60°
Mà ta biết góc A=60°
Hình thang ABED có 2 góc đáy bằng nhau => là hình thang cân
b ,
Ta có :
CE = BE
DF=FA
->EF là đường trung bình của hình bình hành ABCD .
-> AB // EF // CD mà EB // AF ( E , F thuộc AD và BC )
-> Tứ giác ABEF là hình bình hành .
-> EF = AB mà AD = BC = 2AB
-> AD = 2EF
Xét tam giác AED có : đường trung tuyến EF ứng với cạnh huyền AD và
EF = 1/2 AD nên tam giác AED là tam giác vuông tại E
-> Góc AED = 90 độ .

a: Ta có: BC=AD(ABCD là hình bình hành)
\(BE=EC=\dfrac{BC}{2}\)(E là trung điểm của BC)
\(AF=FD=\dfrac{AD}{2}\)(F là trung điểm của AD)
Do đó: BE=EC=AF=FD
Xét tứ giác ABEF có
BE//AF
BE=AF
Do đó: ABEF là hình bình hành
Hình bình hành ABEF có \(BE=BA\left(=\dfrac{BC}{2}\right)\)
nên ABEF là hình thoi
b: Ta có: BE=BA
BA=BI
Do đó: BE=BI
Ta có: BE//AF
=>\(\widehat{IBE}=\widehat{IAF}\)(hai góc đồng vị)
mà \(\widehat{IAF}=60^0\)
nên \(\widehat{IBE}=60^0\)
Xét ΔBIE có BI=BE và \(\widehat{IBE}=60^0\)
nên ΔBIE đều
=>\(\widehat{I}=60^0=\widehat{A}\)
Xét tứ giác AIEF có EF//AI
nên AIEF là hình thang
Hình thang AIEF có \(\widehat{EIA}=\widehat{FAB}\left(cmt\right)\)
nên AIEF là hình thang cân

Xét tứ giác BMCD có
BM//CD
BM=CD
Do đó: BMCD là hình bình hành
Suy ra: Hai đường chéo BC và MD cắt nhau tại trung điểm của mỗi đường
mà E là trung điểm của BC
nên E là trung điểm của MD
hay M,E,D thẳng hàng



Jztr
Ghi cho đủ đề đi bạn]
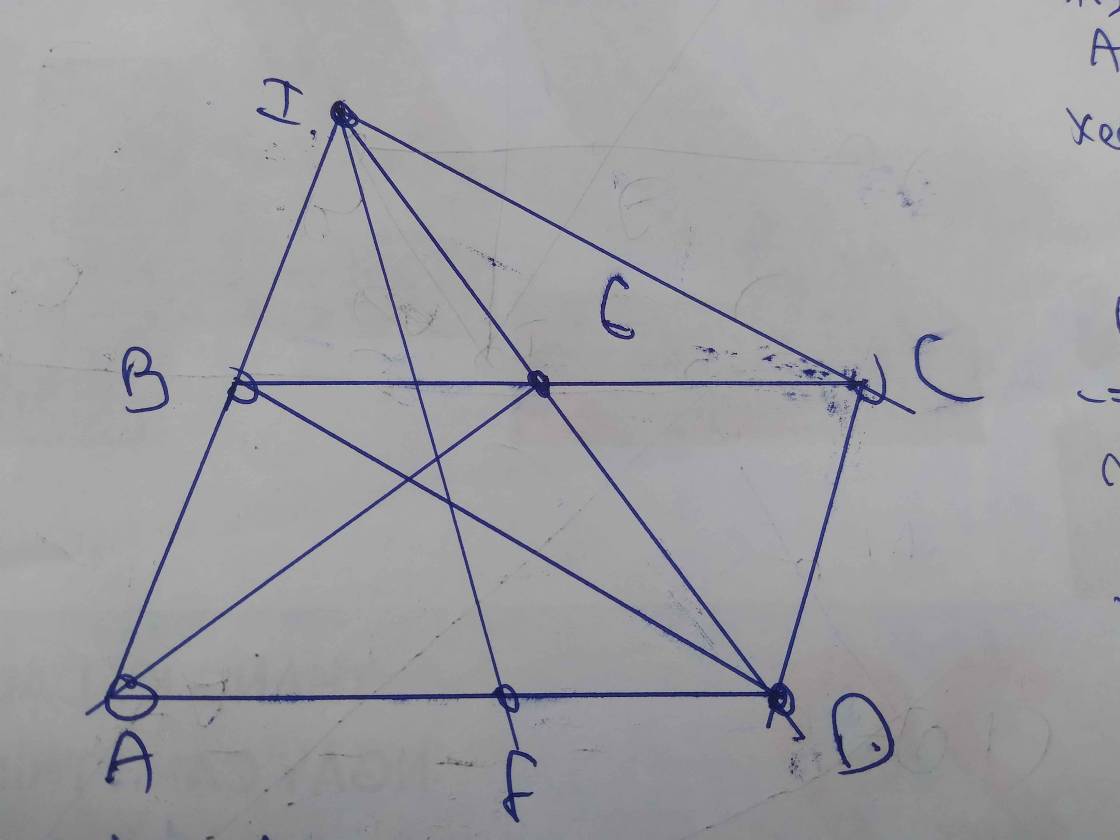
Không ý là vẽ cái hình thôi bạn