Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 2 đường thẳng cắt nhau là xx';yy' , cắt tại O
ta có: đường thẳng xx',yy' cắt nhau tại O
mà góc xOy = 47 độ
=> góc xOy = x'Oy' = 47 độ ( đối đỉnh)
=> góc x'Oy' = 47 độ
mà góc xOy + góc x'Oy = 180 độ ( kề bù)
thay số: 47 độ + góc x'Oy = 180 độ
góc x'Oy = 180 độ - 47 độ
góc x'Oy = 133 độ
mà góc x'Oy = góc xOy' = 133 độ ( đối đỉnh)
=> góc xOy' = 133 độ
x y y' x' 47độ
Hai đường thẳng cắt nhau sẽ tạo thành 2 góc đối đỉnh
\(\Rightarrow\)1 trong 3 góc cò lại sẽ có số đo là 47 độ
1 đường thẳng sẽ có số đo là 180 độ
Vậy góc còn lại có số độ là :
180 - 47 = 133 độ
\(\Rightarrow\)Các góc còn lại sẽ có số đo là : 1 góc 47 độ và 2 góc 133 độ

Vẽ h
Ta chia ra thì góc O1 và O3 đối đỉnh là 30 độ
O2 và O4 thì kê bù
=) O2 và O4 = 150 độ
k nha

47 độ O 1 2 3 4
Ta có:
O2 =O4 = 47 độ( đối đỉnh)
Ta có:
O3+O4 = 180 độ ( kề bù)
=> O3 = 180 độ - O4
O3 = 180 độ - 47 độ
O3 = 133 độ
=> O1 = O3 = 133 độ( đối đỉnh)

o 1 2 3 4
Theo đề bài :
và
đối đỉnh, suy ra :
Ta có và
kề bù suy ra:
+
= 1800
= 1800 -
= 1800 - 470 = 1330
Mà : và
đối đỉnh, suy ra :
=

Trần Khánh Hiền
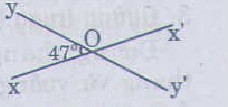
Giả sử hai đường thẳng xx' và yy' cắt nhau tại O và ˆxOy=47∘xOy^=47∘ (hình vẽ bên). Suy ra ˆx′Oy′=ˆxOy=47∘x′Oy′^=xOy^=47∘ (hai góc đối đỉnh).
ˆxOy′=180∘−ˆxOy=180∘−47∘=133∘xOy′^=180∘−xOy^=180∘−47∘=133∘ (do ˆx′Oyx′Oy^ và ˆxOy′xOy′^ kề bù)
Và ˆx′Oy=ˆ
Giả sử hai đường thẳng xx' và yy' cắt nhau tại O và ˆxOy=47∘xOy^=47∘ (hình vẽ bên). Suy ra ˆx′Oy′=ˆxOy=47∘x′Oy′^=xOy^=47∘ (hai góc đối đỉnh).
ˆxOy′=180∘−ˆxOy=180∘−47∘=133∘xOy′^=180∘−xOy^=180∘−47∘=133∘ (do ˆx′Oyx′Oy^ và ˆxOy′xOy′^ kề bù)
Và ˆx′Oy=ˆxOy′=133∘x′Oy^=xOy′^=133∘ (hai góc đối đỉnh).

Vì là đối đỉnh => = nhau, đã thế lại là kề bù => 1800 - 470 = 1330 chứ sao nữa
còn phải vẽ hình nữa bạn ạ như thế chỉ đúng kết quả thôi mà tớ cũng làm được như thế cơ

O y x' x y' 47 0
Giả sử hai đường thẳng \(xx'\)và \(yy'\)cắt nhau tại O và \(\widehat{xOy}=47^0\)
\(\Rightarrow\widehat{x'Oy'}=\widehat{xOy}=47^0\)đối đỉnh
\(\widehat{xOy'}=180^0-\widehat{xOy}=180^0-47^0=133^0\)
do \(\widehat{xOy}\)và \(\widehat{xOy'}\)kề bù và \(\widehat{x'Oy}=\widehat{xOy'}=133^0\)
Bài 2 : Ta có hình vẽ :
y O y' x x' z' z Hình hơi lệch tí nên thông cảm nhé
Các cặp góc bằng nhau là : \(\widehat{xOy}=\widehat{x'Oy'};\widehat{yOz}=\widehat{y'Oz'}\)

O x y x' y' 1 2 3 4
ta gọi hai đường thẳng đó là xx' và yy' cắt nhau tại O
\(\widehat{xOy}=\widehat{O_1}=47\)
ta có góc O1=góc O3 ( đối đỉnh)
ta lại có O1+O2=180 ( hai góc kề bù nhau)
=> góc O2=180-góc O1=180-47=133
mà O2=O4=133 ( đối đỉnh )
OK???
C gửi nè(tích giúp c nha)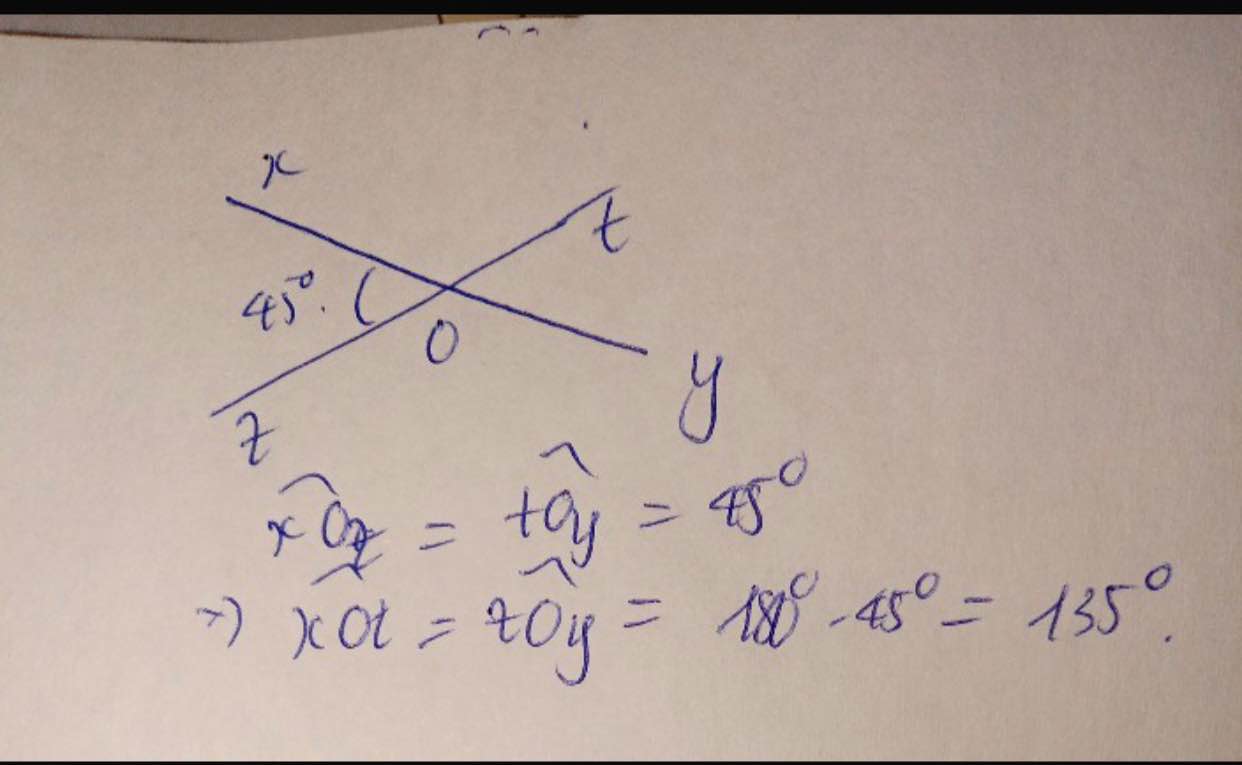
\(47^0;133^0;133^0\)