Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Độ dài của cung tròn có số đo bằng 1 rad là bằng bán kính R.
b) Độ dài l của cung tròn có số đo \(\alpha \) rad: \(l = R\alpha \).

Ta có tam giác OBC đều, đường cao OI = (R√3)/2
⇒ I chạy trên đường tròn tâm O bán kính (R√3)/2.
Vì A cố định, G là trọng tâm tam giác ABC nên A G → = 2 3 A I →
⇒ có phép vị tự tâm A tỉ số k = 2/3 biến đường tròn (O;(R√3)/2) thành đường tròn (O';R’) với R ' = R 3 2 . 2 3 = R 3 3
Chọn đáp án C

Tham khảo:
a) 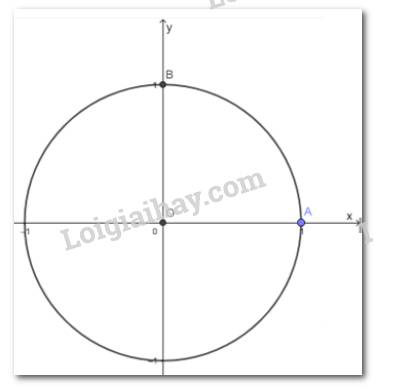
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
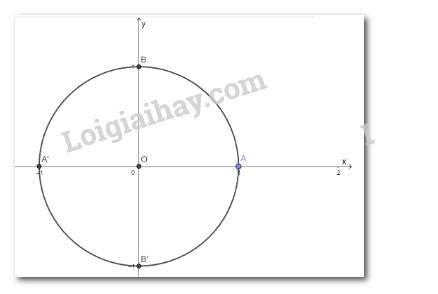

a) \(l = R\alpha = 20.\frac{\pi }{{12}} = \frac{{5\pi }}{3}\)
b) \(l = R\alpha = 20.1,5\pi = 30\pi \)
c) Đổi \({35^0} = 35.\frac{\pi }{{180}} = \frac{7\pi }{36}\)
\(l = R\alpha = 20.\frac{7\pi }{36} = \frac{35\pi }{9}\)
d) Đổi \({315^0} = 315.\frac{\pi }{{180}} = \frac{{7\pi }}{4}\)
\(l = R\alpha = 20.\left( {\frac{{7\pi }}{4}} \right) = 35\pi \)


Gọi (C) là đường tròn tâm O bán kính r, \(\left(C_1\right)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng qua tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \(\left(C_1\right)\).
Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') và \(\left(C_1\right)\).

Đáp án A.
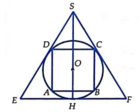
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ SEF đều” (hình vẽ).
![]()
=>Bán kính đáy và chiều cao của hình trụ (T) lần lượt là
![]()
và ![]()
Thể tích khối trụ là
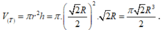
Ta có ∆ SEF đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của ∆ SEF.
Gọi H là trung điểm của EF thì
Hình vuông ABCD nội tiếp đường tròn (O) nên SH = 3OH = 3R![]()
Bán kính đáy và chiều cao của hình nón (N) lần lượt là ![]()
Thể tích khối nón là
![]()
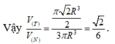
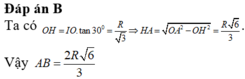

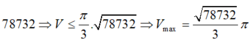
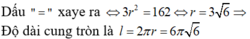
\( \Rightarrow \widehat {AOB} = 60^\circ \)