H
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PN
24 tháng 10 2017
Mafia đề ko thiếu, có mà bn thiếu kiến thức ấy.
Giải:
Gọi A là góc nhọn giữa đt y = 2x-4 với trục Ox ---> tan A = 2 ---> A ~ 63*26'
Gọi B là góc nhọn giữa đt y = -x-2 với trục Ox ---> |tan B| = |-1| = 1 ---> B = 45*
Gọi C là góc nhọn giữa 2 đt y = 2x-4 và y = -x-2.Theo hình vẽ ta có :
A + B + C = 180* ---> C = 180* - A - B = 71*34' ~ 72*
P/s: Nếu sai thì thông cảm
KV
30 tháng 10 2023
a)
b) Phương trình hoành độ giao điểm của hai đường thẳng đã cho:
-3x + 5 = 2x
⇔ 2x + 3x = 5
⇔ 5x = 5
⇔ x = 1 ⇒ y = 2.1 = 2
Vậy M(1; 2)
10 tháng 12 2023
a: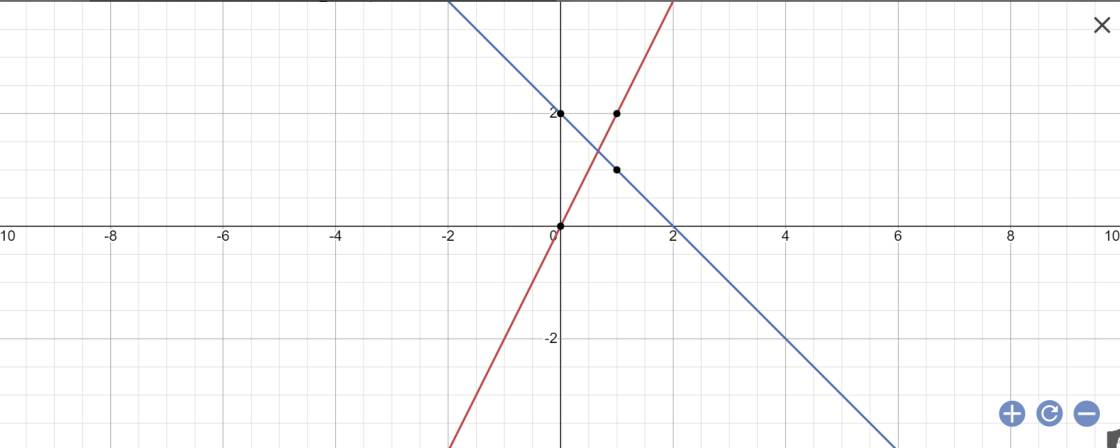 
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
\(b-1=2\)
=>b=2+1=3
24 tháng 11 2021
\(b,\text{PT hoành độ giao điểm: }-2x+5=x-1\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ \text{Vậy }A\left(2;1\right)\text{ là giao điểm }\left(d_1\right)\text{ và }\left(d_2\right)\\ c,\text{Gọi }\left(d_3\right):y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \left(d_3\right)\text{//}\left(d_1\right)\text{ và }M\left(-2;1\right)\in\left(d_3\right)\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne5\\-2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(d_3\right):y=-2x-1\)
9 tháng 1 2022
1: Để hai đường song song thì m+3=2
hay m=-1
Bạn ơi, bạn kí hiệu lại đi bạn. Khó hiểu quá
21 tháng 12 2020
b) Vì C(xC,yC) là giao điểm của hai đường thẳng y=x+2 và y=-2x+5 nên hoành độ của C là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của y=x+2 và y=-2x+5
hay x+2=-2x+5
\(\Leftrightarrow x+2+2x-5=0\)
\(\Leftrightarrow3x-3=0\)
\(\Leftrightarrow3x=3\)
hay x=1
Thay x=1 vào hàm số y=x+2, ta được:
y=1+2=3
Vậy: C(1;3)
Vì A(xA;yA) là giao điểm của đường thẳng y=x+2 với trục hoành nên yA=0
Thay y=0 vào hàm số y=x+2, ta được:
x+2=0
hay x=-2
Vậy: A(-2:0)
Vì B(xB,yB) là giao điểm của đường thẳng y=-2x+5 với trục hoành Ox nên yB=0
Thay y=0 vào hàm số y=-2x+5, ta được:
-2x+5=0
\(\Leftrightarrow-2x=-5\)
hay \(x=\dfrac{5}{2}\)
Vậy: \(B\left(\dfrac{5}{2};0\right)\)
Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(xA-xB\right)^2+\left(yA-yB\right)^2}\)
\(\Leftrightarrow AB=\sqrt{\left(-2-\dfrac{5}{2}\right)^2+\left(0-0\right)^2}\)
\(\Leftrightarrow AB=\sqrt{\left(-\dfrac{9}{2}\right)^2}=\dfrac{9}{2}=4,5\left(cm\right)\)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(xA-xC\right)^2+\left(yA-yC\right)^2}\)
\(\Leftrightarrow AC=\sqrt{\left(-2-1\right)^2+\left(0-3\right)^2}\)
\(\Leftrightarrow AC=\sqrt{18}=3\sqrt{2}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(xB-xC\right)^2+\left(yB-yC\right)^2}\)
\(\Leftrightarrow BC=\sqrt{\left(\dfrac{5}{2}-1\right)^2+\left(0-3\right)^2}\)
\(\Leftrightarrow BC=\sqrt{\dfrac{45}{4}}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)
Chu vi của tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(\Leftrightarrow C_{ABC}=4.5+3\sqrt{2}+\dfrac{3\sqrt{5}}{2}\simeq12.10cm\)
Nửa chu vi của tam giác ABC là:
\(P_{ABC}=\dfrac{C_{ABC}}{2}\simeq\dfrac{12.10}{2}=6.05cm\)
Diện tích của tam giác ABC là:
\(S_{ABC}=\sqrt{P\cdot\left(P-AB\right)\cdot\left(P-BC\right)\cdot\left(P-AC\right)}\)
\(=\sqrt{6.05\cdot\left(6.05-4.5\right)\cdot\left(6.05-3\sqrt{2}\right)\cdot\left(6.05-\dfrac{3\sqrt{5}}{2}\right)}\)
\(\simeq6.76cm^2\)